Câu hỏi:
2 năm trước
Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\) Kẻ \(BE \bot DC\) kéo dài.
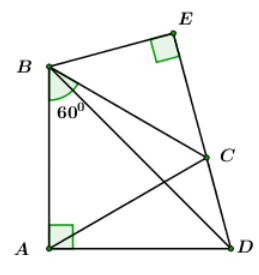
Tính \(CE.\)?
Trả lời bởi giáo viên
Đáp án đúng: d
Áp dụng định lý Pitago cho\(\Delta BEC\) vuông tại \(E\) ta có:
\(\begin{array}{l}EC = \sqrt {B{C^2} - B{E^2}} = \sqrt {{{20}^2} - {{\left( {10\sqrt 2 } \right)}^2}} \\ = 10\sqrt 2 \,\,cm.\end{array}\)
Hướng dẫn giải:
Áp dụng định lý Pitago và các tỉ số lượng giác của góc nhọn để làm bài toán.
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
