Cho hình thang vuông \(ABCD\)  có hai đáy  \(AB = 12\,cm,\,\,DC = 16\,\,cm,\) cạnh xiên \(AD = 8\,cm.\)  Tính các góc và cạnh góc vuông của hình thang.

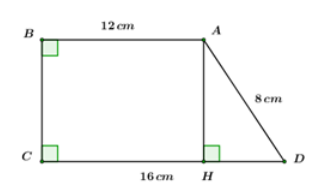
Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\)

Có hình thang vuông \(ABCD\) cạnh xiên  \(AD \Rightarrow \angle ABC = \angle BCD = {90^o}.\)

Dễ thấy \(ABCH\)  là hình chữ nhật (có 3 góc vuông) \( \Rightarrow HC = AB = 12\,cm\)

\( \Rightarrow HD = DC - HC = 16 - 12 = 4\,\,(cm)\)

Áp dụng định lý Pitago cho \(\Delta AHD\)  vuông tại \(H\)  ta có:

\(\begin{array}{l}A{H^2} = A{D^2} - H{D^2} \Rightarrow AH = \sqrt {A{D^2} - H{D^2}}  = \sqrt {{8^2} - {4^2}}  = 4\sqrt 3 \,\,\left( {cm} \right).\\ \Rightarrow BC = AH \approx 6,93\,\,cm\end{array}\) 

Xét \(\Delta AHD\)  vuông tại \(H\) ta có: \(\cos \angle D = \dfrac{{HD}}{{AD}} = \dfrac{1}{2} \Rightarrow \angle D = {60^o}\) 

\(\begin{array}{l} \Rightarrow \angle DAH = {90^o} - \angle D = {30^o}\\ \Rightarrow \angle BAD = \angle BAH + \angle DAH = {90^o} + {30^o} = {120^o}.\end{array}\)