Cho tứ giác \(ABCD\) có \(AB = AC = AD = 20\,\,cm,\,\,\angle B = {60^0}\) và \(\angle A = {90^0}.\)  Kẻ \(BE \bot DC\) kéo dài.

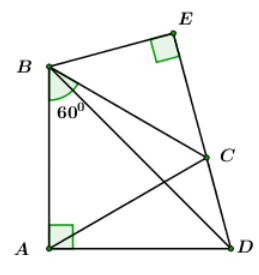
Tính \(BE\)?

Áp dụng định lý Pitago cho \(\Delta ABD\) vuông tại \(A\) ta có:

\(DB = \sqrt {A{B^2} + A{D^2}}  = \sqrt {{{20}^2} + {{20}^2}}  = 20\sqrt 2 \,\,cm.\)

Mà \(\Delta ABD\) có \(AB = AD = 20\,cm \Rightarrow \Delta ABD\) vuông cân tại\(A.\)

\( \Rightarrow \angle ABD = \angle ADB = {45^0}\) (tính chất tam giác cân).

Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = AC = 20\,cm\\\angle ABC = {60^0}\end{array} \right. \Rightarrow \Delta ABC\) là tam giác đều.

\( \Rightarrow BC = 20\,cm;\,\,\,\angle BAC = \angle BCA = {60^0}.\)

Lại có: \(AC = AD = 20\,\,cm \Rightarrow \Delta ACD\) cân tại \(A\)

\(\begin{array}{l} \Rightarrow \angle ACD = \angle ADC = \dfrac{{{{180}^0} - \angle CAD}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - \angle BAC} \right)}}{2} = \dfrac{{{{180}^0} - \left( {{{90}^0} - {{60}^0}} \right)}}{2} = {75^0}.\\ \Rightarrow \angle EDB = \angle ADC - \angle ADB = {75^0} - {45^0} = {30^0}.\end{array}\)

Xét \(\Delta BED\) vuông tại \(E\) ta có:

\(\left\{ \begin{array}{l}BE = BD.\sin \angle EDB = 20\sqrt 2 .\sin {30^0} = 20\sqrt 2 .\dfrac{1}{2} = 10\sqrt 2 \,\,cm.\\ED = BD.cos\angle EDB = 20\sqrt 2 .cos{30^0} = 20\sqrt 2 .\dfrac{{\sqrt 3 }}{2} = 10\sqrt 6 \,\,cm.\end{array} \right.\)