Câu hỏi:
2 năm trước
Cho $A,B,C,D$ là $4$ đỉnh của hình vuông có cạnh là \(a\). Tính diện tích của hình hoa $4$ cánh giới hạn bởi các đường tròn có bán kính bằng \(a\), tâm là các đỉnh của hình vuông.
Trả lời bởi giáo viên
Đáp án đúng: c
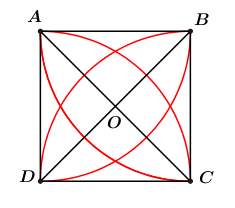
Ta có diện tích của hình hoa cần tình băng $4$ lần diện tích của hình viên phân$AC$: \(S = 4{S_{vp\;AC}}.\)
Có: \({S_{vp\;AC}} = {S_{cung\;AC}} - {S_{ADC}} = \dfrac{{\pi {R^2}{{.90}^0}}}{{{{360}^0}}} - \dfrac{1}{2}{R^2} = \left( {\dfrac{\pi }{4} - \dfrac{1}{2}} \right){R^2} = \dfrac{{\pi - 2}}{4}{a^2}\) \( \Rightarrow S = 4{S_{vp\;AC}} = 4.\dfrac{{\pi - 2}}{4}{a^2} = \left( {\pi - 2} \right){a^2}.\)
Hướng dẫn giải:
Áp dụng công thức tính diện tích cung tròn: \(S = \dfrac{{\pi {R^2}n}}{{360}}.\)

