So sánh \(\widehat {APB}\) và \(\widehat {ABT}\) trong hình vẽ dưới đây biết \(BT\) là tiếp tuyến của đường tròn \(\left( O \right)\).
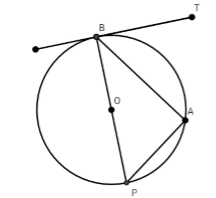
Xét đường tròn \(\left( O \right)\) có \(\widehat {ABT}\) là góc tạo bởi tiếp tuyến \(BT\) và dây cung \(AB\)
\(\widehat {APB}\) là góc nội tiếp chắn cung \(AB\)
Suy ra \(\widehat {ABT} = \widehat {APB}\) (hệ quả).
Hai tam giác nào sau đây đồng dạng?
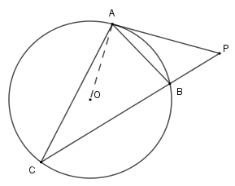
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {BAP}\) (hệ quả) suy ra \(\Delta PAC\backsim\Delta PBA\left( {g - g} \right)\) .
Giả sử \(OA = 3\,cm;MC = 6\,cm\) . Độ dài \(CH\) là
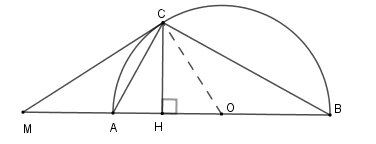
Vì \(OA = 3cm \Rightarrow OC = OA = 3cm\)
Theo định lý Pytago cho tam giác \(MCO\) vuông ta có \(MO = \sqrt {O{C^2} + M{C^2}} = \sqrt {{3^2} + {6^2}} = 3\sqrt 5 \,cm\)
Xét tam giác \(MCO\) vuông tại \(C,\) theo hệ thức lượng trong tam giác vuông ta có \(MC.CO = CH.MO \Rightarrow CH = \dfrac{{MC.CO}}{{MO}} = \dfrac{{6.3}}{{3\sqrt 5 }} = \dfrac{{6\sqrt 5 }}{5}\left( {cm} \right)\) .
Tam giác \(IKA\) đồng dạng với tam giác
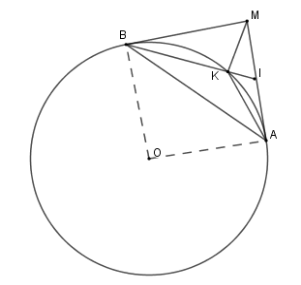
Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Giả sử \(\widehat {CBA} = 30^\circ \) . Chọn câu sai.
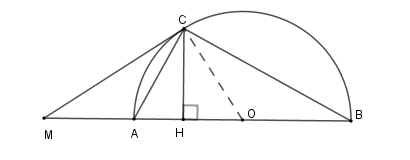
Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA} = 30^\circ \) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(\widehat {CAB} = 90^\circ - \widehat {CBA} = 90^\circ - 30^\circ = 60^\circ \) (do \(\Delta CAB\) vuông tại \(C\))
Lại có \(\widehat {ACH} + \widehat {CAB} = 90^\circ \Rightarrow \widehat {ACH} = 90^\circ - 60^\circ = 30^\circ \)
\(\widehat {CBA}\) là góc nội tiếp chắn cung \(CA \Rightarrow \widehat {COA} = 2\widehat {CBA} = 2.30^\circ = 60^\circ \) .
Vậy A, B, D đúng, C sai.
Tam giác \(AMB\) đồng dạng với tam giác
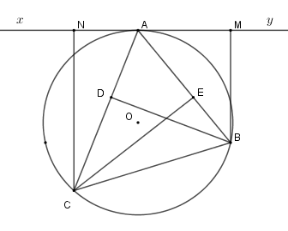
Xét \(\left( O \right)\) có \(\widehat {MAB} = \widehat {ACB}\) (hệ quả) \( \Rightarrow \Delta AMB\backsim\Delta CDB\left( {g - g} \right)\)
Giả sử \(\widehat {CBA} = 30^\circ \) . Chọn câu sai.

Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA} = 30^\circ \) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) suy ra \(\widehat {CAB} = 90^\circ - \widehat {CBA} = 90^\circ - 30^\circ = 60^\circ \) (do \(\Delta CAB\) vuông tại \(C\))
Lại có \(\widehat {ACH} + \widehat {CAB} = 90^\circ \Rightarrow \widehat {ACH} = 90^\circ - 60^\circ = 30^\circ \)
\(\widehat {CBA}\) là góc nội tiếp chắn cung \(CA \Rightarrow \widehat {COA} = 2\widehat {CBA} = 2.30^\circ = 60^\circ \) .
Vậy A, B, D đúng, C sai.
Giả sử \(\dfrac{{BA}}{{BC}} = \dfrac{1}{2}\). Khi đó
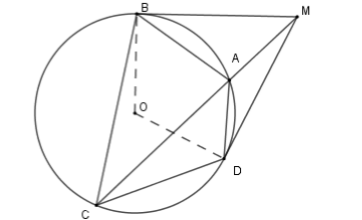
Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{BA}}{{CB}}\)
Mà theo câu trước ta có \(\dfrac{{MD}}{{MC}} = \dfrac{{AD}}{{CD}}\)
Theo tính chất hai tiếp tuyến cắt nhau thì \(MB = MD\) nên \(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}} = \dfrac{1}{2}\)
Chọn câu đúng
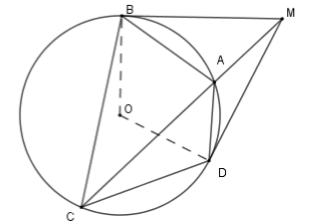
Xét \(\left( O \right)\) có \(\widehat {MDA} = \widehat {DCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AD\) )
Suy ra \(\Delta MAD\backsim\Delta MDC\left( {g - g} \right) \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MD}}{{MC}} = \dfrac{{DA}}{{CD}} \Rightarrow MA.MC = M{D^2}\)
Chọn câu đúng

Xét \(\left( O \right)\) có \(\widehat {MDA} = \widehat {DCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AD\) )
Suy ra \(\Delta MAD\backsim\Delta MDC\left( {g - g} \right) \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MD}}{{MC}} = \dfrac{{DA}}{{CD}} \Rightarrow MA.MC = M{D^2}\)
Tia phân giác trong góc $M$ cắt $NP$ và \((O)\) lần lượt tại $I$ và $D$. Chọn câu đúng?
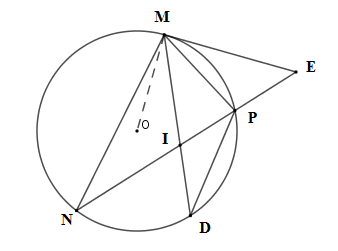
Vì \(MD\) là tia phân giác \(\widehat {NMP}\) nên \(\widehat {NMD} = \widehat {DMP}\) suy ra cung \(PD = \) cung \(PN.\)
Xét $\Delta DPM$ và \(\Delta NIM\) có \(\widehat {MNI} = \widehat {IDP}\) (hai góc nội tiếp cùng chắn cung \(MP\)) và \(\widehat {NMI} = \widehat {IPD}\) (cmt)
Nên \(\Delta DPM\backsim\Delta NIM\left( {g - g} \right)\) nên A đúng, B sai.
Xét \(\Delta IPD\) và \(\Delta PMD\) có \(\widehat D\,\) chung và \(\widehat {IPD} = \widehat {IMP}\) (hai góc nội tiếp chắn hai cung bằng nhau)
Nên \(\Delta IPD \backsim \Delta PMD\left( {g - g} \right)\) suy ra C, D sai.
Tích \(EP.EN\) bằng
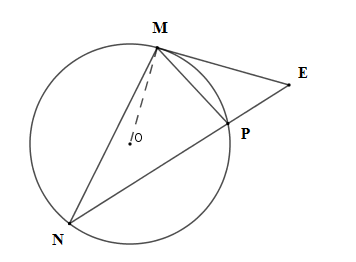
Xét \(\left( O \right)\) có \(\widehat {MNP} = \widehat {EMP}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(MP\) )
Xét \(\Delta EPM\) và \(\Delta EMN\) có \(\widehat E\) chung và \(\widehat {MNP} = \widehat {EMP}\)
suy ra \(\Delta EPM\backsim\Delta EMN\left( {g - g} \right)\) suy ra \(\dfrac{{EP}}{{EM}} = \dfrac{{EM}}{{EN}} \Leftrightarrow EP.EN = E{M^2} = {4^2} = 16\,\left( {c{m^2}} \right)\) .
Tích \(EP.EN\) bằng

Xét \(\left( O \right)\) có \(\widehat {MNP} = \widehat {EMP}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(MP\) )
Xét \(\Delta EPM\) và \(\Delta EMN\) có \(\widehat E\) chung và \(\widehat {MNP} = \widehat {EMP}\)
suy ra \(\Delta EPM\backsim\Delta EMN\left( {g - g} \right)\) suy ra \(\dfrac{{EP}}{{EM}} = \dfrac{{EM}}{{EN}} \Leftrightarrow EP.EN = E{M^2} = {4^2} = 16\,\left( {c{m^2}} \right)\) .
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) có \(AC = 3cm\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(C\) kẻ \(CM{\rm{//}}xy\left( {M \in AB} \right)\) . Chọn câu đúng.
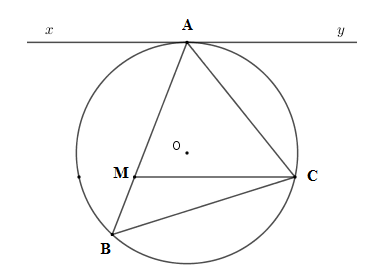
Ta có \(\widehat {yAC} = \widehat {ABC}\) (hệ quả góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) ) mà \(\widehat {yAC} = \widehat {ACM}\) (so le trong) nên \(\widehat {ABC} = \widehat {ACM} \Rightarrow \Delta AMC\backsim\Delta ACB\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AC}} = \dfrac{{AC}}{{AB}} \Rightarrow AM.AB = A{C^2} = {3^2} = 9\left( {c{m^2}} \right)\) .
Hệ thức nào dưới đây đúng .
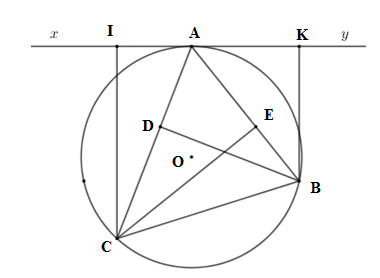
Từ câu trước ta có \(\Delta IAC\backsim\Delta EBC \Rightarrow \dfrac{{IA}}{{EB}} = \dfrac{{AC}}{{BC}}\)
Tương tự ta có \(\Delta AKB\backsim\Delta CDB\left( {g - g} \right) \Rightarrow \dfrac{{CD}}{{AK}} = \dfrac{{BC}}{{AB}}\)
Suy ra \(\dfrac{{IA}}{{EB}}.\dfrac{{CD}}{{AK}} = \dfrac{{AC}}{{BC}}.\dfrac{{BC}}{{AB}}\)\( \Leftrightarrow \dfrac{{IA}}{{EB}}.\dfrac{{CD}}{{AK}} = \dfrac{{AC}}{{AB}}\)
Tam giác \(IAC\) đồng dạng với tam giác
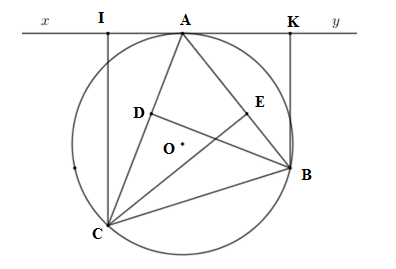
Xét \(\left( O \right)\) có \(\widehat {IAC} = \widehat {ABC}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC)\)
Xét hai tam giác vuông \(IAC\) và \(EBC\) có \(\widehat {IAC} = \widehat {ABC}\) (cmt) \( \Rightarrow \Delta IAC\backsim\Delta EBC\left( {g - g} \right)\)
Tam giác \(IAC\) đồng dạng với tam giác

Xét \(\left( O \right)\) có \(\widehat {IAC} = \widehat {ABC}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC)\)
Xét hai tam giác vuông \(IAC\) và \(EBC\) có \(\widehat {IAC} = \widehat {ABC}\) (cmt) \( \Rightarrow \Delta IAC\backsim\Delta EBC\left( {g - g} \right)\)
Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung?
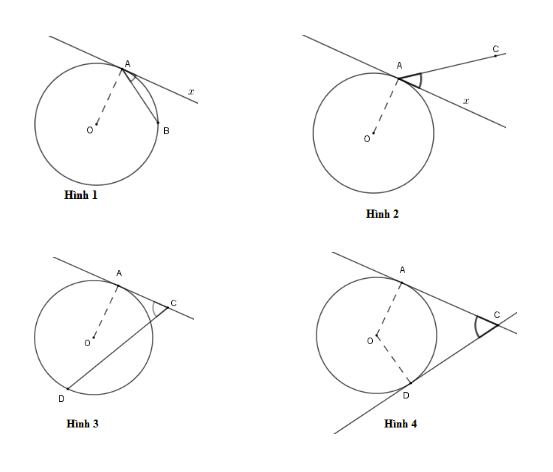
Cho đường tròn tâm \((O)\) có \(Ax\) là tia tiếp tuyến tại tiếp điểm $A$ và dây cung $AB.$ Khi đó, góc \(BAx\)là góc tạo bởi tia tiếp tuyến và dây cung.
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng
Góc tạo bởi tiếp tuyến và dây cung có số đo bằng nửa số đo cung bị chắn
Kết luận nào sau đây là đúng.
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

