Giả sử $\widehat {CBA} = 30^\circ$ . Chọn câu sai.

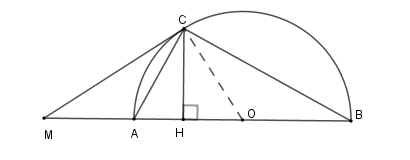
Xét nửa $\left( O \right)$ có $\widehat {MCA} = \widehat {CBA} = 30^\circ$  (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung $AC$ )

Lại có $\widehat {ACB} = 90^\circ$ (góc nội tiếp chắn nửa đường tròn) suy ra $\widehat {CAB} = 90^\circ  - \widehat {CBA} = 90^\circ  - 30^\circ  = 60^\circ$ (do $\Delta CAB$ vuông tại $C$)

 Lại có $\widehat {ACH} + \widehat {CAB} = 90^\circ  \Rightarrow \widehat {ACH} = 90^\circ  - 60^\circ  = 30^\circ$

$\widehat {CBA}$ là góc nội tiếp chắn cung $CA \Rightarrow \widehat {COA} = 2\widehat {CBA} = 2.30^\circ  = 60^\circ$ .

Vậy A, B, D đúng, C sai.