Trả lời bởi giáo viên
Đáp án đúng: b
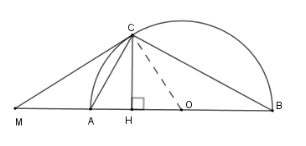
Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .

