Trả lời bởi giáo viên
Đáp án đúng: a
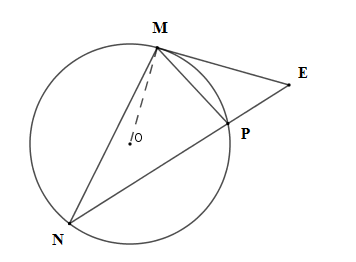
Xét \(\left( O \right)\) có \(\widehat {MNP} = \widehat {EMP}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(MP\) )
Xét \(\Delta EPM\) và \(\Delta EMN\) có \(\widehat E\) chung và \(\widehat {MNP} = \widehat {EMP}\)
suy ra \(\Delta EPM\backsim\Delta EMN\left( {g - g} \right)\) suy ra \(\dfrac{{EP}}{{EM}} = \dfrac{{EM}}{{EN}} \Leftrightarrow EP.EN = E{M^2} = {4^2} = 16\,\left( {c{m^2}} \right)\) .
Hướng dẫn giải:
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng theo trường hợp góc – góc.

