Câu hỏi:
2 năm trước
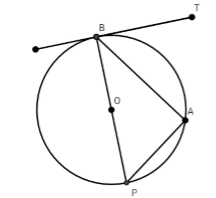
So sánh \(\widehat {APB}\) và \(\widehat {ABT}\) trong hình vẽ dưới đây biết \(BT\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Trả lời bởi giáo viên
Đáp án đúng: a
Xét đường tròn \(\left( O \right)\) có \(\widehat {ABT}\) là góc tạo bởi tiếp tuyến \(BT\) và dây cung \(AB\)
\(\widehat {APB}\) là góc nội tiếp chắn cung \(AB\)
Suy ra \(\widehat {ABT} = \widehat {APB}\) (hệ quả).
Hướng dẫn giải:
Sử dụng hệ quả của góc tạo bởi tia tiếp tuyến và dây cung:
‘Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.’

