Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) . Trên tia đối của tia \(AB\) lấy điểm \(M\) . Vẽ tiếp tuyến \(MC\) với nửa đường tròn. Gọi \(H\) là hình chiếu của \(C\) trên \(AB\) .
\(CA\) là tia phân giác của góc nào dưới đây
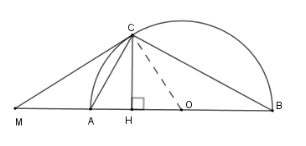
Xét nửa $\left( O \right)$ có \(\widehat {MCA} = \widehat {CBA}\) (*) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\) )
Lại có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Xét tam giác \(ACH\) vuông tại \(H\) có \(\widehat {ACH}+ \widehat {CAH}=90^0\) (1)
Xét tam giác \(ACB\) vuông tại \(C\) có \(\widehat {CBA}+ \widehat {CAH}=90^0\) (2)
Từ (1) và (2) suy ra \(\widehat {ACH} = \widehat {CBA}\) (**) (cùng phụ với góc \(\widehat {CAB}\) )
Từ (*) và (**) ta có \(\widehat {MCA} = \widehat {ACH}\) nên \(CA\) là tia phân giác của góc \(\widehat {MCH}\) .
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) . Trên tia đối của tia \(AB\) lấy điểm \(M\) . Vẽ tiếp tuyến \(MC\) với nửa đường tròn. Gọi \(H\) là hình chiếu của \(C\) trên \(AB\) .
Giả sử \(OA = a;MC = 2a\) . Độ dài \(CH\) là
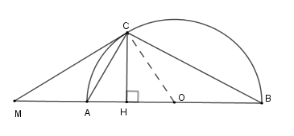
Theo định lý Pytago cho tam giác \(MCO\) vuông ta có \(MO = \sqrt {O{C^2} + M{C^2}} = a\sqrt 5 \)
Xét tam giác \(MCO\) vuông ta có \(MC.CO = CH.MO \Rightarrow CH = \dfrac{{2{a^2}}}{{\sqrt 5 a}} = \dfrac{{2\sqrt 5 a}}{5}\) .
Từ điểm \(M\) nằm ngoài \(\left( O \right)\) kẻ các tiếp tuyến \(MD;MB\) và cát tuyến \(MAC\) với đường tròn. (\(A\) nằm giữa \(M\) và \(C\) )
Khi đó \(MA.MC\) bằng
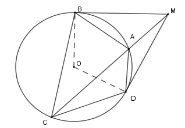
Xét \(\left( O \right)\) có \(\widehat {MBA} = \widehat {BCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AB\) )
Suy ra \(\Delta MBA\backsim\Delta MCB\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{MB}}{{MC}} = \dfrac{{MA}}{{MB}} = \dfrac{{BA}}{{CB}} \)
\(\Rightarrow MA.MC = M{B^2}\)
Từ điểm \(M\) nằm ngoài \(\left( O \right)\) kẻ các tiếp tuyến \(MD;MB\) và cát tuyến \(MAC\) với đường tròn. (\(A\) nằm giữa \(M\) và \(C\) )
Hệ thức nào dưới đây là đúng.
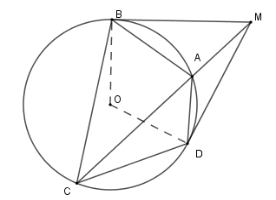
Tương tự câu trước ta có \(\Delta MAD\backsim \Delta MDC\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MD}}{{MC}} = \dfrac{{AD}}{{DC}}\)
Mà theo câu trước ta có \(\dfrac{{MB}}{{MC}} = \dfrac{{BA}}{{CB}}\)
Theo tính chất hai tiếp tuyến cắt nhau thì \(MB = MD\) nên \(\dfrac{{AD}}{{DC}} = \dfrac{{AB}}{{BC}} \Leftrightarrow AD.BC = AB.DC\)
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\), tiếp tuyến tại ${\rm{A}}$ của\((O)\) cắt $BC$ tại $P$ .
Hai tam giác nào sau đây đồng dạng?
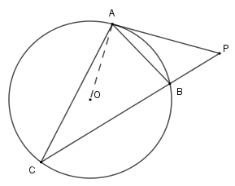
Xét \(\left( O \right)\) có \(\widehat {ACB} = \widehat {BAP}\) (hệ quả) suy ra \(\Delta PAC\backsim\Delta PBA\left( {g - g} \right)\) .
Cho tam giác \(ABC\) nội tiếp đường tròn \((O)\), tiếp tuyến tại ${\rm{A}}$ của\((O)\) cắt $BC$ tại $P$ .
Tia phân giác trong góc $A$ cắt $BC$ và \((O)\) lần lượt tại $D$ và $M$. Khi đó \(MA.MD\) bằng
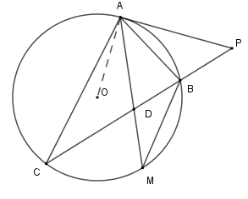
Xét đường tròn \((O)\) có \(\widehat {MBC} = \widehat {MAC}\) (hai góc nội tiếp cùng chắn cung MC)
Lại có \(\widehat {MAB} = \widehat {MAC}\) (do AM là phân giác góc BAC)
Suy ra \(\widehat {MBD} = \widehat {MAB}\) (cùng bằng \(\widehat {MAC}\) )
Xét \(\Delta MBD\) và \(\Delta MAB\) có \(\widehat M\) chung và \(\widehat {MBD} = \widehat {MAB}\) (chứng minh trên)
Nên \(\Delta MBD\backsim\Delta MAB\left( {g - g} \right) \)\(\Rightarrow \dfrac{{MB}}{{MA}} = \dfrac{{MD}}{{MB}} \)\(\Rightarrow MA.MD = M{B^2}\)
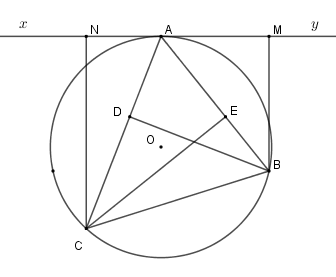
Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó
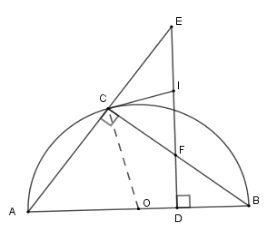
Xét \(\left( O \right)\) có $\widehat {ICB} = \widehat {CAB}$ (hệ quả) mà $\widehat {BFD} = \widehat {BAC}$ (cùng phụ với \(\widehat {ABC}\) )
Nên \(\widehat {ICF} = \widehat {BFD} \Rightarrow \widehat {ICF} = \widehat {CFI}\) suy ra \(\Delta ICF\) cân tại \(I \Rightarrow IF = IC\) (*)
Lại có \(\widehat {ICE} + \widehat {ICF} = 90^\circ \Rightarrow \widehat {ICE} + \widehat {CAB} = 90^\circ \) mà \(\widehat {CAB} + \widehat {AED} = 90^\circ \Rightarrow \widehat {CEI} = \widehat {ECI} \Rightarrow \Delta ICE\) cân tại \(I\)
Nên \(IE = IC\) (**)
Từ (*) và (**) suy ra \(IE = IF = \dfrac{{EF}}{2}\) .
Cho đường tròn $(O;R)$ với $A$ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $Ax$ với $(O)$ và lấy $M$ là điểm bất kì thuộc tia $Ax$. Vẽ tiếp tuyến thứ hai $MB$ với đường tròn $(O)$. Gọi $I$ là trung điểm $MA$, $K$ là giao điểm của $BI$ với $(O)$.
Tam giác \(IKA\) đồng dạng với tam giác
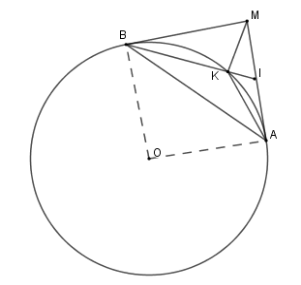
Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Cho đường tròn $(O;R)$ với $A$ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $Ax$ với $(O)$ và lấy $M$ là điểm bất kì thuộc tia $Ax$. Vẽ tiếp tuyến thứ hai $MB$ với đường tròn $(O)$. Gọi $I$ là trung điểm $MA$, $K$ là giao điểm của $BI$ với $(O)$.
Tam giác nào dưới đây đồng dạng với tam giác \(IKM\)?
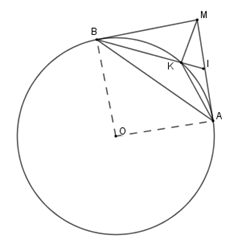
\(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\) (câu trước) \( \Rightarrow \dfrac{{IK}}{{IA}} = \dfrac{{IA}}{{IB}}\) mà \(IA = IM \Rightarrow \dfrac{{IK}}{{IM}} = \dfrac{{IM}}{{IB}}\) nên \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\)
Cho đường tròn $(O;R)$ với $A$ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $Ax$ với $(O)$ và lấy $M$ là điểm bất kì thuộc tia $Ax$. Vẽ tiếp tuyến thứ hai $MB$ với đường tròn $(O)$. Gọi $I$ là trung điểm $MA$, $K$ là giao điểm của $BI$ với $(O)$.
Giả sử $MK$cắt $(O)$ tại $C$. Đường thẳng \(MA\) song song với đường thẳng
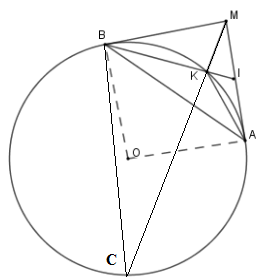
Vì \(\Delta IKM\backsim\Delta IMB\left( {c - g - c} \right)\) \( \Rightarrow \widehat {IMK} = \widehat {MBI}\) mà \(\widehat {MBI} = \widehat {MCB}\) (hệ quả)
Nên \(\widehat {BCM} = \widehat {CMA}\) mà hai góc ở vị trí so le trong nên \(MA{\rm{//}}BC\) .
Cho tam giác nhọn \(ABC\) nội tiếp \(\left( O \right)\) . Kẻ tiếp tuyến \(xAy\) với \(\left( O \right)\) . Từ \(B\) kẻ \(BM{\rm{//}}xy\left( {M \in AC} \right)\) . Khi đó tích $AM.AC$ bằng
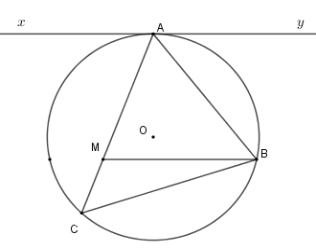
Ta có \(\widehat {yAB} = \widehat {ACB}\) (hệ quả) mà \(\widehat {yAB} = \widehat {ABM}\) (so le trong) nên \(\widehat {ACB} = \widehat {ABM} \Rightarrow \Delta AMB\backsim\Delta ABC\left( {g - g} \right)\)
\(\dfrac{{AM}}{{AB}} = \dfrac{{AB}}{{AC}} \Rightarrow AM.AC = A{B^2}\) .
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\) nội tiếp \(\left( {O;R} \right)\) . Gọi \(BD;CE\) là hai đường cao của tam giác. Gọi \(d\) là tiếp tuyến tại \(A\) của \(\left( {O;R} \right)\) và \(M,N\) lần lượt là hình chiếu của \(B,C\) trên \(d\) .
Tam giác \(AMB\) đồng dạng với tam giác
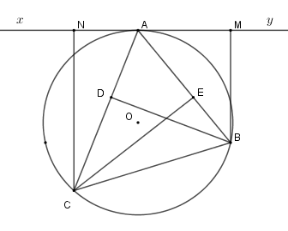
Xét \(\left( O \right)\) có \(\widehat {MAB} = \widehat {ACB}\) (hệ quả) \( \Rightarrow \Delta AMB\backsim\Delta CDB\left( {g - g} \right)\)
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\) nội tiếp \(\left( {O;R} \right)\) . Gọi \(BD;CE\) là hai đường cao của tam giác. Gọi \(d\) là tiếp tuyến tại \(A\) của \(\left( {O;R} \right)\) và \(M,N\) lần lượt là hình chiếu của \(B,C\) trên \(d\) .
Hệ thức nào dưới đây đúng .
Từ câu trước, ta có \(\dfrac{{AM}}{{CD}} = \dfrac{{AB}}{{CB}}\)
Tương tự ta có \(\Delta ANC\backsim\Delta BEC\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{BE}}{{AN}} = \dfrac{{BC}}{{AC}}\)
Suy ra \(\dfrac{{AM}}{{CD}}.\dfrac{{BE}}{{AN}} = \dfrac{{AB}}{{BC}}.\dfrac{{BC}}{{AC}}\)
\(\Leftrightarrow \dfrac{{AB}}{{AC}} = \dfrac{{MA.BE}}{{NA.CD}}\)
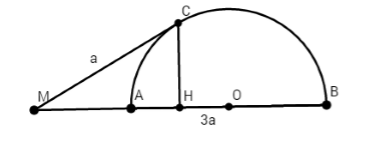
Cho nửa đường tròn $\left( O \right)$ đường kính $AB$. Trên tia đối của tia $AB$ lấy một điểm $M$. Vẽ tiếp tuyến $MC$ với nửa đường tròn. Gọi $H$ là hình chiếu của $C$ lên $AB$. Biết $MC = a,MB = 3a$. Độ dài đường kính $AB$ là?
Ta có \(\widehat {MCA} = \widehat {CBA}\) (cùng chắn cung \(AC\))
Xét \(\Delta ACM\) và \(\Delta CBM\) có:
\(\widehat {MCA} = \widehat {CBA}\) (cmt)
\(\widehat M\) chung
Suy ra \(\Delta ACM \backsim \Delta CBM\) (g.g)
$\begin{array}{l} \Rightarrow M{C^2} = MA.MB\\ \Rightarrow MA = \dfrac{{{a^2}}}{{3a}} = \dfrac{a}{3}\\ \Rightarrow AB = MB - MA = 3a - \dfrac{a}{3} = \dfrac{{8a}}{3}\end{array}$
cho đường tròn $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc. Gọi $I$ là điểm trên cung $AC$ sao cho khi vẽ tiếp tuyến qua $I$ và cắt $DC$ kéo dài tại $M$ thì \(\widehat {CIM} = {30^0}\). Số đo góc $AOI$ là:
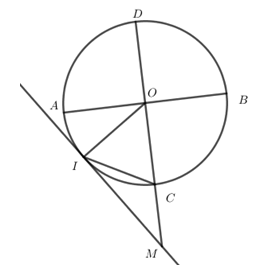
Ta có: \(\widehat {CIM}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung $IC$
\(\widehat {IOC}\) là góc ở tâm chắn cung $IC$
\(\begin{array}{l} \Rightarrow \widehat {CIM} = \dfrac{1}{2}\widehat {IOC} \Rightarrow \widehat {IOC} = 2\widehat {CIM} = {2.30^0} = {60^0}\\ \Rightarrow \widehat {IOA} = {90^0} - {60^0} = {30^0}\end{array}\)
Cho đường tròn $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc. Gọi $I$ là điểm trên cung $AC$ sao cho khi vẽ tiếp tuyến qua $I$ và cắt $DC$ kéo dài tại $M$ thì $IC = CM$. Độ dài $OM$ tính theo bán kính là:
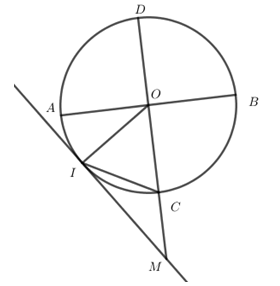
+) Ta có: \(\widehat {CIM} = \dfrac{1}{2}\widehat {IOC}\) (góc tạo bởi tiếp tuyến và dây cung với góc ở tâm chắn cung $IC$)
\( \Rightarrow \widehat {IOC} = 2\widehat {CIM}\).
Lại có \(\widehat {OCI} = \widehat {CIM} + \widehat {CMI} = 2\widehat {CIM}\) (do \(\Delta CMI\) cân tại \(C\))
Do đó \(\Delta OIC\) đều (vì \(\widehat {OIC}=\widehat {IOC}=\widehat {OCI}\)) \( \Rightarrow \widehat {IOM} = {60^0}\).
+) Xét \(\Delta OIM\) vuông tại \(I\) có:
\(\cos \widehat {IOM} = \dfrac{{OI}}{{OM}} = \dfrac{R}{{OM}} = \dfrac{1}{2} \Rightarrow OM = 2R\).
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A$ và $B$. Một đường thẳng tiếp xúc với $\left( O \right)$ tại $C$, và tiếp xúc với đường tròn $\left( {O'} \right)$ tại $D$ sao cho tia \(AB\) cắt đoạn \(CD\). Vẽ đường tròn $\left( I \right)$ đi qua ba điểm $A,C,D$ cắt đường thẳng $AB$ tại một điểm thứ hai là $E$. Chọn câu đúng:
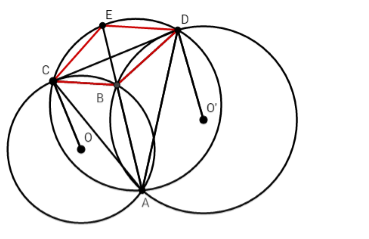
+) Xét $\left( O \right)$ ta có:
\(\widehat {BAC} = \widehat {BCD}\) (cùng chắn cung $CB$)
Xét $\left( I \right)$ có:
\(\widehat {CAB} = \widehat {EDC}\) (cùng chắn cung \(CE\))
\( \Rightarrow \widehat {BCD} = \widehat {EDC} \Rightarrow ED//BC\left( 1 \right)\)
+) Xét $\left( {O'} \right)$ có:
\(\widehat {BAD} = \widehat {BDC}\) (cùng chắn cung $BD$)
Xét $\left( I \right)$ có:
\(\widehat {EAD} = \widehat {ECD}\) (cùng chắn cung $ED$)
\( \Rightarrow \widehat {ECD} = \widehat {BDC} \Rightarrow CE//BD\left( 2 \right)\)
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $BDEC$ là hình bình hành

