Câu hỏi:
3 năm trước
Cho nửa đường tròn \(\left( O \right)\) đường kính \(AB\) . Trên tia đối của tia \(AB\) lấy điểm \(M\) . Vẽ tiếp tuyến \(MC\) với nửa đường tròn. Gọi \(H\) là hình chiếu của \(C\) trên \(AB\) .
Giả sử \(OA = a;MC = 2a\) . Độ dài \(CH\) là
Trả lời bởi giáo viên
Đáp án đúng: c
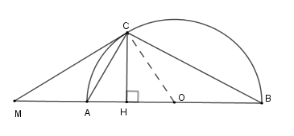
Theo định lý Pytago cho tam giác \(MCO\) vuông ta có \(MO = \sqrt {O{C^2} + M{C^2}} = a\sqrt 5 \)
Xét tam giác \(MCO\) vuông ta có \(MC.CO = CH.MO \Rightarrow CH = \dfrac{{2{a^2}}}{{\sqrt 5 a}} = \dfrac{{2\sqrt 5 a}}{5}\) .
Hướng dẫn giải:
Sử dụng định lý Pytago và hệ thức lượng trong tam giác vuông

