Cho nửa đường tròn $(O)$ đường kính $AB$ và một điểm $C$ trên nửa đường tròn. Gọi $D$ là một điểm trên đường kính $AB$; qua $D$ kẻ đường vuông góc với $AB$ cắt $BC$ tại $F$, cắt $AC$ tại $E$. Tiếp tuyến của nửa đường tròn tại $C$cắt $EF$ tại $I.$Khi đó

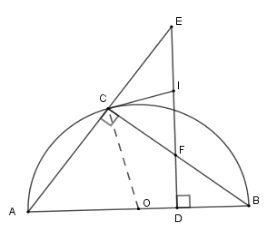
Xét \(\left( O \right)\) có $\widehat {ICB} = \widehat {CAB}$  (hệ quả) mà $\widehat {BFD} = \widehat {BAC}$ (cùng phụ với \(\widehat {ABC}\) )

Nên \(\widehat {ICF} = \widehat {BFD} \Rightarrow \widehat {ICF} = \widehat {CFI}\) suy ra \(\Delta ICF\) cân tại \(I \Rightarrow IF = IC\) (*)

Lại có \(\widehat {ICE} + \widehat {ICF} = 90^\circ  \Rightarrow \widehat {ICE} + \widehat {CAB} = 90^\circ \) mà \(\widehat {CAB} + \widehat {AED} = 90^\circ  \Rightarrow \widehat {CEI} = \widehat {ECI} \Rightarrow \Delta ICE\) cân tại \(I\)

Nên \(IE = IC\) (**)

Từ (*) và (**) suy ra \(IE = IF = \dfrac{{EF}}{2}\) .