Câu hỏi:
2 năm trước
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ cắt nhau tại $A$ và $B$. Một đường thẳng tiếp xúc với $\left( O \right)$ tại $C$, và tiếp xúc với đường tròn $\left( {O'} \right)$ tại $D$ sao cho tia \(AB\) cắt đoạn \(CD\). Vẽ đường tròn $\left( I \right)$ đi qua ba điểm $A,C,D$ cắt đường thẳng $AB$ tại một điểm thứ hai là $E$. Chọn câu đúng:
Trả lời bởi giáo viên
Đáp án đúng: b
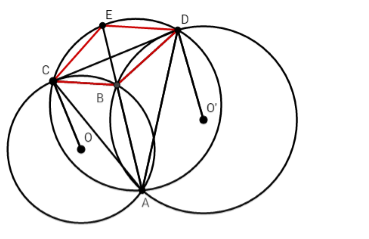
+) Xét $\left( O \right)$ ta có:
\(\widehat {BAC} = \widehat {BCD}\) (cùng chắn cung $CB$)
Xét $\left( I \right)$ có:
\(\widehat {CAB} = \widehat {EDC}\) (cùng chắn cung \(CE\))
\( \Rightarrow \widehat {BCD} = \widehat {EDC} \Rightarrow ED//BC\left( 1 \right)\)
+) Xét $\left( {O'} \right)$ có:
\(\widehat {BAD} = \widehat {BDC}\) (cùng chắn cung $BD$)
Xét $\left( I \right)$ có:
\(\widehat {EAD} = \widehat {ECD}\) (cùng chắn cung $ED$)
\( \Rightarrow \widehat {ECD} = \widehat {BDC} \Rightarrow CE//BD\left( 2 \right)\)
Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $BDEC$ là hình bình hành
Hướng dẫn giải:
Sử dụng các tính chất: góc nội tiếp cùng chắn một cung; góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn một cung.
Sử dụng dấu hiệu nhận biết một hình là hình bình hành, hình thoi, hình chữ nhật, hình vuông.
