Câu hỏi:
3 năm trước
cho đường tròn $\left( {O;R} \right)$ có hai đường kính $AB$ và $CD$ vuông góc. Gọi $I$ là điểm trên cung $AC$ sao cho khi vẽ tiếp tuyến qua $I$ và cắt $DC$ kéo dài tại $M$ thì \(\widehat {CIM} = {30^0}\). Số đo góc $AOI$ là:
Trả lời bởi giáo viên
Đáp án đúng: d
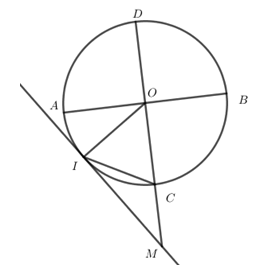
Ta có: \(\widehat {CIM}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung $IC$
\(\widehat {IOC}\) là góc ở tâm chắn cung $IC$
\(\begin{array}{l} \Rightarrow \widehat {CIM} = \dfrac{1}{2}\widehat {IOC} \Rightarrow \widehat {IOC} = 2\widehat {CIM} = {2.30^0} = {60^0}\\ \Rightarrow \widehat {IOA} = {90^0} - {60^0} = {30^0}\end{array}\)
Hướng dẫn giải:
Tính \(\widehat {IOC} \Rightarrow \widehat {IOA}\) .

