Câu hỏi:
2 năm trước
Cho đường tròn $(O;R)$ với $A$ là điểm cố định trên đường tròn. Kẻ tiếp tuyến $Ax$ với $(O)$ và lấy $M$ là điểm bất kì thuộc tia $Ax$. Vẽ tiếp tuyến thứ hai $MB$ với đường tròn $(O)$. Gọi $I$ là trung điểm $MA$, $K$ là giao điểm của $BI$ với $(O)$.
Tam giác \(IKA\) đồng dạng với tam giác
Trả lời bởi giáo viên
Đáp án đúng: b
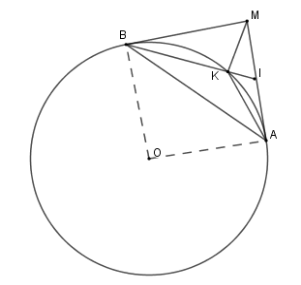
Ta có \(\widehat {IAK} = \widehat {IBA}\) (hệ quả) nên \(\Delta IKA\backsim\Delta IAB\left( {g - g} \right)\)
Hướng dẫn giải:
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.

