Câu hỏi:
3 năm trước
Cho tam giác nhọn \(ABC\) \(\left( {AB < AC} \right)\) nội tiếp \(\left( {O;R} \right)\) . Gọi \(BD;CE\) là hai đường cao của tam giác. Gọi \(d\) là tiếp tuyến tại \(A\) của \(\left( {O;R} \right)\) và \(M,N\) lần lượt là hình chiếu của \(B,C\) trên \(d\) .
Hệ thức nào dưới đây đúng .
Trả lời bởi giáo viên
Đáp án đúng: d
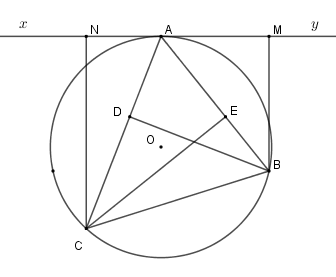
Từ câu trước, ta có \(\dfrac{{AM}}{{CD}} = \dfrac{{AB}}{{CB}}\)
Tương tự ta có \(\Delta ANC\backsim\Delta BEC\left( {g - g} \right) \)
\(\Rightarrow \dfrac{{BE}}{{AN}} = \dfrac{{BC}}{{AC}}\)
Suy ra \(\dfrac{{AM}}{{CD}}.\dfrac{{BE}}{{AN}} = \dfrac{{AB}}{{BC}}.\dfrac{{BC}}{{AC}}\)
\(\Leftrightarrow \dfrac{{AB}}{{AC}} = \dfrac{{MA.BE}}{{NA.CD}}\)
Hướng dẫn giải:
Sử dụng câu trước và các tam giác đồng dạng

