Trả lời bởi giáo viên
Đáp án đúng: d
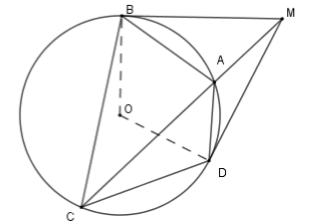
Xét \(\left( O \right)\) có \(\widehat {MDA} = \widehat {DCA}\) (góc tạo bởi tiếp tuyến và dây cung \(AB\) bằng góc nội tiếp chắn cung \(AD\) )
Suy ra \(\Delta MAD\backsim\Delta MDC\left( {g - g} \right) \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MD}}{{MC}} = \dfrac{{DA}}{{CD}} \Rightarrow MA.MC = M{D^2}\)
Hướng dẫn giải:
Sử dụng hệ quả góc tạo bởi tia tiếp tuyến và dây cung để chứng minh hai góc bằng nhau và suy ra hai tam giác đồng dạng.

