Tia phân giác trong góc $M$ cắt $NP$ và \((O)\) lần lượt tại $I$ và $D$. Chọn câu đúng?

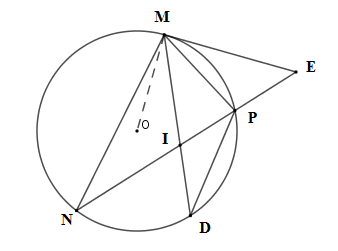
Vì \(MD\) là tia phân giác \(\widehat {NMP}\) nên \(\widehat {NMD} = \widehat {DMP}\)  suy ra cung \(PD = \) cung \(PN.\)

Xét $\Delta DPM$ và \(\Delta NIM\) có \(\widehat {MNI} = \widehat {IDP}\)  (hai góc nội tiếp cùng chắn cung \(MP\)) và \(\widehat {NMI} = \widehat {IPD}\)  (cmt)

Nên \(\Delta DPM\backsim\Delta NIM\left( {g - g} \right)\) nên A đúng, B sai.

Xét \(\Delta IPD\) và \(\Delta PMD\) có \(\widehat D\,\) chung và \(\widehat {IPD} = \widehat {IMP}\) (hai góc nội tiếp chắn hai cung bằng nhau)

Nên \(\Delta IPD \backsim \Delta PMD\left( {g - g} \right)\) suy ra C, D sai.