Câu hỏi:
2 năm trước
Cho đường tròn $\left( {O;R} \right)$, dây cung $AB = R\sqrt 2 $. Vẽ đường kính $CD \bot AB$ ($C$ thuộc cung lớn $AB$). Trên cung $AC$ nhỏ lấy điểm $M$, vẽ dây $AN{\rm{//}}CM$. Độ dài đoạn $MN$ là
Trả lời bởi giáo viên
Đáp án đúng: d
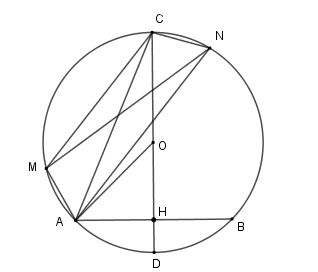
Vì hai dây $MC{\rm{//}}AN$ nên hai cung $AM$ và cung $CN$ bằng nhau, hay $AM = CN$
Suy ra $MCNA$ là hình thang cân $ \Rightarrow MN = AC$.
Gọi $H$ là giao của $CD$ và $AB$. Khi đó vì $AB \bot CD$ tại $H$ nên $H$ là trung điểm của $AB \Rightarrow AH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 2 }}{2}$
Xét tam giác vuông $AHO$, theo định lý Pytago ta có $OH = \sqrt {A{O^2} - A{H^2}} = \sqrt {{R^2} - {{\left( {\dfrac{{R\sqrt 2 }}{2}} \right)}^2}} = \dfrac{{R\sqrt 2 }}{2}$
$ \Rightarrow CH = R + \dfrac{{R\sqrt 2 }}{2} = \dfrac{{2 + \sqrt 2 }}{2}R$
Theo định lý Pytago cho tam giác $ACH$ vuông ta có $AC = \sqrt {C{H^2} + A{H^2}} = \sqrt {\dfrac{{{{\left( {2 + \sqrt 2 } \right)}^2}}}{4}{R^2} + \dfrac{{2{R^2}}}{4}} = \sqrt {\dfrac{{8 + 4\sqrt 2 }}{4}{R^2}} = \sqrt {2 + \sqrt 2 } .R$
Vậy $MN = R\sqrt {2 + \sqrt 2 } $.
Hướng dẫn giải:
Sử dụng tính chất hai cung bị chắn giữa hai dây song song thì bằng nhau
Sử dụng mối liên hệ giữa dây và đường kính
Sử dụng định lý Pytago
