Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết $\widehat E = {25^0}$, số đo góc $\widehat {AIC}$ là:
Trả lời bởi giáo viên
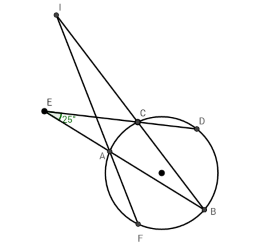
B nằm chính giữa cung $DF$ nên sđ $\overparen {BD}$ = sđ$\overparen {BF}$
Mặt khác góc tại E và I là hai góc có đỉnh bên ngoài đường tròn nên
$\begin{array}{l}\widehat E = \dfrac{1}{2}\left( {sđ\overparen {BD} - sđ \overparen{AC}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen {BF} - sđ\overparen {AC}} \right) = \widehat I\end{array}$
Theo đề bài ta có
$\widehat E = \widehat I = {25^0}$
Hướng dẫn giải:
Sử dụng: Góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

