Cho \(\left( {O;R} \right)\) có hai đường kính \(AB,CD\) vuông góc với nhau. Trên đường kính \(AB\) lấy điểm \(E\) sao cho \(AE = R\sqrt 2 \) . Vẽ dây \(CF\) đi qua \(E\) . Tiếp tuyến của đường tròn tại \(F\) cắt đường thẳng \(CD\) tại \(M\) , dây \(AF\) cắt \(CD\) tại \(N\) . Tính độ dài \(ON\) theo \(R.\)
Trả lời bởi giáo viên
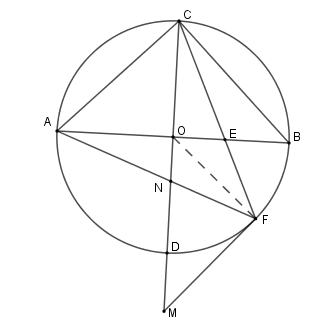
Xét \(\Delta AOC\) vuông cân tại \(O\) có \(AC = \sqrt {O{A^2} + O{C^2}} = R\sqrt 2 \Rightarrow AO = AE\) nên \(\Delta AEC\) cân tại \(A \Rightarrow \widehat {ACE} = \widehat {AEC}\)
Hay \(\dfrac{1}{2}\) (số đo cung \(AD + \) số đo cung \(DF\) ) \( = \dfrac{1}{2}\) (số đo cung \(AC + \) số đo cung \(BF\) ) mà cung \(AD = \) cung \(AC\)
Nên cung \(DF\) \( = \) cung \(BF\).
Lại có cung \(DF\)\( = \) cung \(BF\) nên \(\widehat {NOF} = \widehat {EOF} \Rightarrow \widehat {AOF} = \widehat {COF}\)
Suy ra \(\Delta OAF = \Delta OCF\left( {c - g - c} \right) \Rightarrow \widehat {OFE} = \widehat {OFN}\)
Suy ra \(\Delta OEF = \Delta ONF\left( {g - c - g} \right) \Rightarrow ON = OE = \left( {\sqrt 2 - 1} \right)R\)
Hướng dẫn giải:
+ Sử dụng góc có đỉnh bên ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn để chứng minh các góc bằng nhau
+ Sử dụng các tam giác bằng nhau

