Câu hỏi:
3 năm trước
Cho tam giác ABC cân tại A, nội tiếp trong (O). Trên cung nhỏ AC, lấy điểm D. Gọi S là giao điểm của AD và BC, I là giao điểm của AC và BD. Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
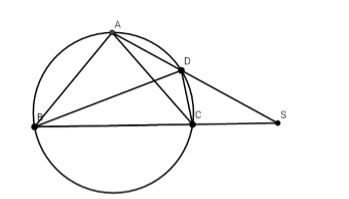
Ta có $\widehat {{\rm{AS}}C}$ là góc có đỉnh nằm ngoài đường tròn nên
$\widehat {{\rm{AS}}C}$=$\dfrac{1}{2}\left( {sđ\overparen{AB} - sđ\overparen{CD}} \right)$
$ = \dfrac{1}{2}\left( {sđ\overparen{AC} - sđ\overparen{CD}} \right)$$ = \dfrac{1}{2}sđ\overparen{AD}$
$ = \widehat {ABD} = \widehat {DCA}$
Hướng dẫn giải:
+) Nhận biết được góc có đỉnh nằm ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn

