Bài tập ôn tập chương 2

Xét phương trình hoành độ giao điểm:

 $\begin{array}{l}\dfrac{1}{2}x - 3 =  - x + 3 \Leftrightarrow \dfrac{3}{2}x = 6 \Leftrightarrow x = 4\\ \Rightarrow y =  - 4 + 3 =  - 1.\end{array}$

Vậy giao điểm cần tìm có tọa độ $(-4;1)$.

Xét phương trình hoành độ giao điểm của $d$ và $d'$ :

$ - 4x + m + 1 = \dfrac{4}{3}x + 15 - 3m \Leftrightarrow \dfrac{{ - 16}}{3}x = 14 - 4m \Leftrightarrow x = \dfrac{{3(4m - 14)}}{{16}}$

$d$ cắt $d'$  tại điểm nằm trên trục tung $ \Leftrightarrow x = \dfrac{{3(4m - 14)}}{{16}} = 0 \Leftrightarrow 4m - 14 = 0 \Leftrightarrow m = \dfrac{7}{2}.$

Ta có $d \cap d' \Leftrightarrow m - 3 \ne 2 \Leftrightarrow m \ne 5$.

Xét phương trình hoành độ của $d'$ và $d''$ :

$\begin{array}{l}2x - 1 = (m - 3)x + 2 \Leftrightarrow (m - 5)x =  - 3 \Leftrightarrow x = \dfrac{{ - 3}}{{m - 5}}\\ \Rightarrow y = \dfrac{{ - 6}}{{m - 5}} - 1 = \dfrac{{ - m - 1}}{{m - 5}}\end{array}$

Theo đề bài: $x.y > 0 \Leftrightarrow \dfrac{{ - 3}}{{m - 5}}.\dfrac{{ - m - 1}}{{m - 5}} > 0 \Leftrightarrow \dfrac{{3(m + 1)}}{{{{(m - 5)}^2}}} > 0$

Mà ${(m - 5)^2} > 0,\forall m \ne 5$

Suy ra $m >  - 1$

Kết hợp điều kiện ta có: $\left\{ \begin{array}{l}m >  - 1\\m \ne 5\end{array} \right.$.

$\left( d \right):{\rm{ 2}}y + x - 7 = 0 \Leftrightarrow y =  - \dfrac{1}{2}x + \dfrac{7}{2}$

Xét phương trình hoành độ giao điểm của $\left( {d'} \right)$ và $\left( {d''} \right)$ : $ - \dfrac{1}{2}x + \dfrac{7}{2} = 3 \Leftrightarrow  - \dfrac{1}{2}x =  - \dfrac{1}{2} \Leftrightarrow x = 1$  nên tọa độ giao điểm là $(1;3)$

Để $\left( d \right);\left( {d'} \right);\left( {d''} \right)$  đồng quy thì $\left( {1;3} \right) \in \left( {d''} \right) \Leftrightarrow 3 = 1.m - 1 \Leftrightarrow m = 4$

Vậy với $m = 4$  thì $\left( d \right);\left( {d'} \right);\left( {d''} \right)$  đồng quy.

Xét phương trình hoành độ giao điểm của $d$ và $d'$:

$2x + m + 3 =  - 4x - m - 2 \Leftrightarrow 6x =  - 2m - 5 $$\Leftrightarrow x = \dfrac{{ - 2m - 5}}{6}$

$ \Rightarrow y = 2.\dfrac{{ - 2m - 5}}{6} + m + 3 $$= \dfrac{{m + 4}}{3}$

Ta có $d$ cắt $d'$  tại điểm thuộc trục hoành nên: $y = \dfrac{{m + 4}}{3} = 0 \Leftrightarrow m =  - 4.$

Vậy $m =  - 4$.

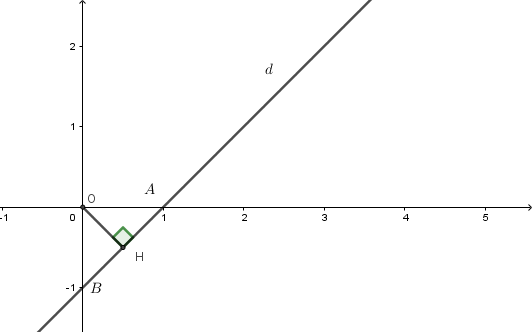
Ta có:

$d \cap Ox$ tại $A(1;0) \Rightarrow OA = 1$

$d \cap Oy $ tại $ B(0; - 1) \Rightarrow OB = 1$

Ta có $OA \bot OB$. Gọi $H$ là hình chiếu của $O$ trên đường thẳng $AB$.

Áp dụng hệ thức trong tam giác ta có:

$\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} = \dfrac{1}{1} + \dfrac{1}{1} = 2\\ \Rightarrow OH = \dfrac{{\sqrt 2 }}{2}\end{array}$

Đường thẳng $d$ vuông góc với đường thẳng $d' \Rightarrow a.\dfrac{{ - 1}}{3} =  - 1 \Leftrightarrow a = 3$

Đường thẳng $d$ đi qua điểm $P(1;-1) \Rightarrow 3.1 + b =  - 1 \Leftrightarrow b =  - 4$

$ \Rightarrow d:y = 3x - 4$.

Gọi $d:y = {\rm{ax}} + b$ đi qua $2$ điểm $M\left( { - 3;2} \right)$ và $N\left( {1; - 1} \right)$

$M$ thuộc $d \Leftrightarrow  - 3a + b = 2 \Rightarrow b = 2 + 3a\,\,\,\,\,(1)$

$N$ thuộc $d \Leftrightarrow 1.a + b =  - 1 \Rightarrow b = - 1 - a \,\,\,\,\,(2)$

Từ (1) và (2) suy ra \(2 + 3a = - 1 - a \Leftrightarrow 4a = - 3 \Leftrightarrow a = - \dfrac{3}{4}\)\( \Rightarrow b = 2 + 3a = - \dfrac{1}{4}\)

Nên $a = \dfrac{{ - 3}}{4};b =  - \dfrac{1}{4}$.

Vậy $d:y =  - \dfrac{3}{4}x - \dfrac{1}{4}$.

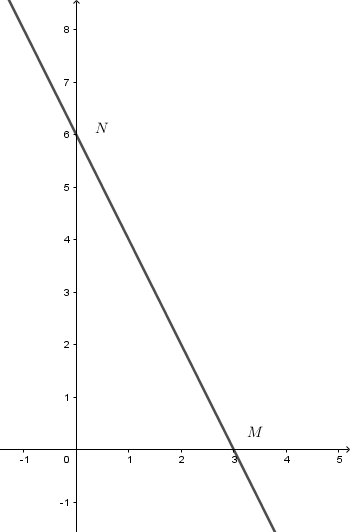
Ta có:

$\begin{array}{l}d' \cap Ox = M(3;0) \Rightarrow OM = 3\\d' \cap Oy = N(0;6) \Rightarrow ON = 6\end{array}$

Ta có tam giác $OMN$ vuông tại $O$.

Áp dụng định lý Py ta go ta có:

$M{N^2} = O{M^2} + O{N^2} = 9 + 36 = 45 \Rightarrow MN = 3\sqrt 5 $

Suy ra chu vi tam giác $OMN$ là: $MN + OM + ON = 3\sqrt 5  + 3 + 6 = 9 + 3\sqrt 5 $

Xét phương trình hoành độ giao điểm của $d$ và $d'$ ta có 

$2x - 1 = x - 3 \Leftrightarrow x =  - 2 \Rightarrow y =  - 5 \Rightarrow M( - 2; - 5)$

Trước hết xét $M$ có thuộc đường thẳng $y = 3x + 1$ không?

Ta có $3.{x_M} + 1 = 3.( - 2) + 1 =  - 5 = {y_M}$ nên $M$ thuộc đồ thị hàm số $y=3x+1$ hay A đúng.

Điểm $\left( {3;2} \right)$ thuộc đường thẳng $y = {\rm{a}}x + b \Rightarrow 3a + b = 2$

Ta có $6a + 2b = 2(3a + b) = 2.2 = 4$

Đồ thị hàm số $y = {\rm{ax}} + b$ cắt trục hoành tại điểm có hoành độ bằng $1$  và cắt trục tung tại điểm có tung độ bằng $2$

$ \Rightarrow \left\{ \begin{array}{l}1.a + b = 0\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 2\\b = 2\end{array} \right.$

Điểm \(A\left( {2; - 1} \right) \in d:y = ax + b \Leftrightarrow 2a + b =  - 1\)

Điểm \(M \in d':2x + y = 3\) có \(x = 0,5 \Rightarrow 2.0,5 + y = 3 \Leftrightarrow y = 2 \Rightarrow M\left( {\dfrac{1}{2};2} \right)\).

\(M\left( {\dfrac{1}{2};2} \right) \in d \Leftrightarrow \dfrac{1}{2}a + b = 2\)

Do đó \(\left\{ \begin{array}{l}2a + b =  - 1\\\dfrac{1}{2}a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} b =  - 1-2a\\b = 2-\dfrac{1}{2}a\end{array} \right. \)\(\Rightarrow  - 1 - 2a = 2 - \dfrac{1}{2}a \Leftrightarrow \dfrac{3}{2}a = - 3 \Leftrightarrow a = - 2\)

Vậy \(a =  - 2\).

$\begin{array}{l}d:mx + 2y = 5 \Rightarrow y = \dfrac{{ - m}}{2}x + \dfrac{5}{2}\\d \cap d' \Leftrightarrow  - \dfrac{m}{2} \ne  - 2 \Leftrightarrow m \ne 4.\end{array}$

Xét phương trình hoành độ giao điểm của $d$ và $d'$ :

$\dfrac{{ - m}}{2}x + \dfrac{5}{2} =  - 2x + 1 \Leftrightarrow \dfrac{{4 - m}}{2}x =  - \dfrac{3}{2} $$\Leftrightarrow x = \dfrac{3}{{m - 4}} \Rightarrow y=-2.\dfrac{3}{{m - 4}}-1 = \dfrac{{m - 10}}{{m - 4}}$

Do $d$ cắt $d'$  tại điểm nằm ở góc phần tư thứ nhất nên ta có: $\left\{ \begin{array}{l}x > 0\\y > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{3}{{m - 4}} > 0\\\dfrac{{m - 10}}{{m - 4}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 4\\m > 10\end{array} \right. \Leftrightarrow m > 10$

Kết hợp điều kiện suy ra $m > 10$ thỏa mãn yêu cầu đề bài.

Xét phương trình hoành độ giao điểm của $d$ và $d'$ : $12x + 5 - m = 3x + m + 3 \Leftrightarrow 9x = 2m - 2 \Leftrightarrow x = \dfrac{{2m - 2}}{9}$

Do $d$ cắt $d'$  tại điểm nằm bên trái trục tung nên ta có: $x < 0 \Leftrightarrow \dfrac{{2m - 2}}{9} < 0 \Leftrightarrow 2m - 2 < 0 \Leftrightarrow m < 1.$

Ta có:

$d \cap Ox $ tại $A( - 3;0) \Rightarrow OA = 3$

$d \cap Oy $ tại $B(0;6) \Rightarrow OB = 6$

Ta có $OA \bot OB$.

Diện tích tam giác $AOB$ là: $\dfrac{1}{2}.3.6 = 9(đv{\rm{d}}t)$

Để \(d:\,\,y = \left( {m + 1} \right)x + 6\) cắt đường thẳng \(y = 5x + m - 2\) tại một điểm nằm trên trục tung thì \(m + 1 \ne 5\) và phương trình hoành độ giao điểm của hai đường thẳng có nghiệm \(x = 0\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m + 1 \ne 5\\\left( {m + 1} \right).0 + 6 = 5.0 + m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\6 = m - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 4\\m = 8\end{array} \right. \Leftrightarrow m = 8\,\,\,\left( {tmđk\,\,m \ne  - 1} \right)\end{array}\)

Vậy \(m = 8\) là giá trị cần tìm.

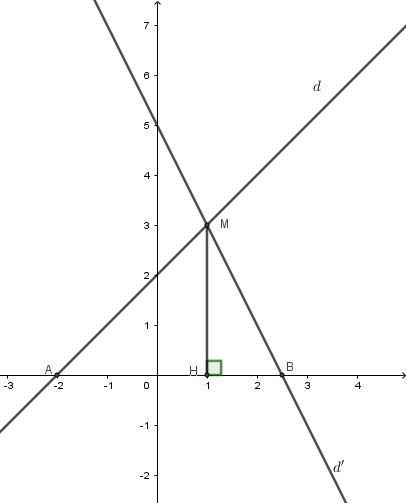
Xét phương trình hoành độ giao điểm của ${d_1};{d_2}$

$x + 2 =  - 2x + 5 \Leftrightarrow x = 1 \Rightarrow y = 3 \Rightarrow {d_1} \cap {d_2}$ tại $ M(1;3)$

Gọi $H$ là chân đường vuông góc kẻ từ $M$ tới $Ox$. Suy ra $MH = 3$

$d \cap Ox$ tại $ A( - 2;0) \Rightarrow OA = 2$

$d' \cap Ox$ tại $ B\left( {\dfrac{5}{2};0} \right) \Rightarrow OB = \dfrac{5}{2}$

$\Rightarrow AB = OA+OB=2 + \dfrac{5}{2} = \dfrac{9}{2}$

${S_{MAB}} = \dfrac{1}{2}AB.MH = \dfrac{1}{2}.\dfrac{9}{2}.3 = \dfrac{{27}}{4}\,(dvdt)$

Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\):

\(2x - 3 =  - \dfrac{1}{2}x + 2 \Leftrightarrow 2x + \dfrac{1}{2}x = 2 + 3 \Leftrightarrow \dfrac{5}{2}x = 5 \Leftrightarrow x = 2\)

Thay \(x = 2\) vào hàm số \(y = 2x - 3\) ta được \(y = 2.2 - 3 = 1.\)

Vậy tọa độ giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(A\left( {2;1} \right)\).

Ba đường thẳng \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy  \( \Rightarrow \left( {{d_3}} \right)\) đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)\( \Rightarrow A \in \left( {{d_3}} \right)\)

Thay tọa độ điểm \(A\)  vào hàm số \(\left( {{d_3}} \right):\,\,y = 3x - 2m - 3\) ta được:

\(1 = 3.2 - 2m - 3\)\( \Rightarrow 2m = 6 - 3 - 1 \Rightarrow m = 1\)

Vậy \(m = 1\) thì ba đường thẳng  \(\left( {{d_1}} \right)\) , \(\left( {{d_2}} \right)\) và \(\left( {{d_3}} \right):y = 3x - 2m - 3\) đồng quy.

Giả sử $MN:y = {\rm{ax}} + b$

Ta có $N$ thuộc $MN \Rightarrow 0 = a.1 + b \Rightarrow a =  - b$;

$M$ thuộc $MN \Rightarrow 2 = a.0 + b \Rightarrow b = 2 \Rightarrow a =  - 2$ $\Rightarrow b=2$

Do đó $MN:y =  - 2{\rm{x}} + 2$.

Vì $M,N$ lần lượt là trung điểm của các cạnh $BC,CA$ của tam giác $ABC$ nên $MN$ là đường trung bình của tam giác $ABC \Rightarrow MN//AB$

Suy ra $AB$ có dạng: $y =  - 2x + b'\,(b' \ne 2)$

Vì $P$ là trung điểm của $AB$ nên $AB$ đi qua $P\left( { - 1; - 1} \right)$

$ \Rightarrow  - 1 =  - 2( - 1) + b' \Leftrightarrow b' =  - 3(t/m)$

Vậy $AB:y =  - 2x - 3.$