Câu hỏi:
2 năm trước
Cho đường thẳng $d':y = - 2x + 6$. Gọi $M,N$ lần lượt là giao điểm của $d'$ với $Ox$ và $Oy$. Khi đó chu vi tam giác $OMN$ là:
Trả lời bởi giáo viên
Đáp án đúng: b
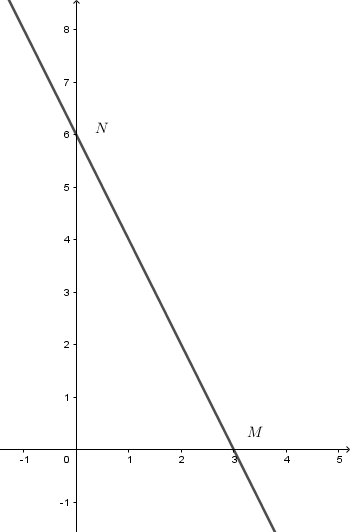
Ta có:
$\begin{array}{l}d' \cap Ox = M(3;0) \Rightarrow OM = 3\\d' \cap Oy = N(0;6) \Rightarrow ON = 6\end{array}$
Ta có tam giác $OMN$ vuông tại $O$.
Áp dụng định lý Py ta go ta có:
$M{N^2} = O{M^2} + O{N^2} = 9 + 36 = 45 \Rightarrow MN = 3\sqrt 5 $
Suy ra chu vi tam giác $OMN$ là: $MN + OM + ON = 3\sqrt 5 + 3 + 6 = 9 + 3\sqrt 5 $
Hướng dẫn giải:
- Tìm giao điểm của đường thẳng với trục hoành, trục tung
- Áp dụng định lý Py-ta-go để tính độ dài đoạn thẳng.
- Sử dụng công thức chu vi tam giác.

