Một hình trụ có thể tích \(V\) không đổi. Hỏi bán kính đáy bằng bao nhiêu để diện tích toàn phần của hình trụ đó là nhỏ nhất.
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là \(R,\,\,h\,\,\left( {R > 0;\,h > 0} \right)\)
Ta có \(V = \pi {R^2}h \Rightarrow h = \dfrac{V}{{\pi {R^2}}}\)
Diện tích toàn phần của hình trụ \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi R.\dfrac{V}{{\pi {R^2}}} + 2\pi {R^2} = \dfrac{{2V}}{R} + 2\pi {R^2}\)
\( = \dfrac{V}{R} + \dfrac{V}{R} + 2\pi {R^2}\mathop \ge \limits_{\cos i} 3\sqrt[3]{{\dfrac{V}{R}.\dfrac{V}{R}.2\pi {R^2}}} = 3\sqrt[3]{{2\pi {V^2}}}\)
Dấu “=” xảy ra \( \Leftrightarrow \dfrac{V}{R} = 2\pi {R^2} \Rightarrow R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)
Vậy với \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\) thì \({S_{tp}}\) đạt giá trị nhỏ nhất là \(3\sqrt[3]{{2\pi {V^2}}}\).
Cho hình trụ bị cắt bỏ một phần \(OABB'A'O'\) như hình vẽ. Thể tích phần còn lại là:
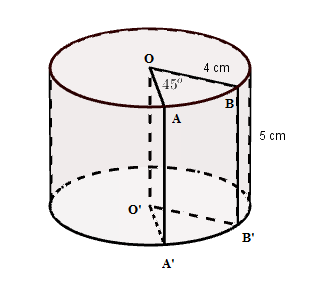
Phần hình trụ bị cắt đi chiếm \(\dfrac{{45^\circ }}{{360^\circ }} = \dfrac{1}{8}\) (hình trụ)
Thể tích phần còn lại là \(V = \dfrac{7}{8}\pi {R^2}h = \dfrac{7}{8}\pi {.4^2}.5 = 70\pi \,\,\left( {c{m^3}} \right)\)
Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$
Chọn khẳng định sai.
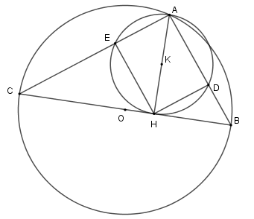
Xét \(\left( O \right)\) có $\widehat {CAD} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn)
Xét \(\left( K \right)\) có \(\widehat {AEH} = \widehat {ADH} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên tứ giác $ADHE$ là hình chữ nhật ( vì có ba góc vuông)\( \Rightarrow \) phương án A đúng.
Xét tam giác vuông \(AHB\) có \(A{H^2} = AD.AB \Rightarrow \) phương án C đúng
Xét tam giác vuông \(A{H^2} = AC.AE\) nên \(AD.AB = AC.AE \Rightarrow \) phương án B đúng
Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$
Biết $BC = 25cm$ và $AH = 12cm.$ Hãy tính diện tích xung quanh của hình tạo thành bởi khi cho tứ giác $ADHE$ quay quanh $AD.$
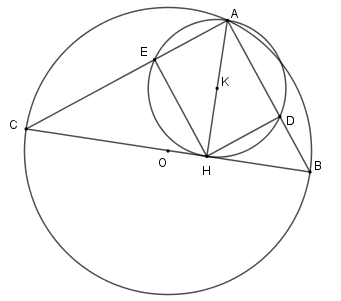
Xét tam giác vuông \(ABC\) có \(HB.HC = A{H^2} \Leftrightarrow HB.HC = 144\) và \(HB + HC = BC \Leftrightarrow HB + HC = 25\)
Suy ra \(HB = 9\,cm;\,HC = 16\,cm\) (Chú ý: $AB < AC$ nên $HB < HC$).
Xét tam giác vuông \(AHB\) có \(\dfrac{1}{{H{D^2}}} = \dfrac{1}{{A{H^2}}} + \dfrac{1}{{H{B^2}}} \Rightarrow HD = \dfrac{{36}}{5}\,cm\)
Tương tự ta có $HE = \dfrac{{48}}{5}cm \Rightarrow AD = \dfrac{{48}}{5}\,cm$.
Khi quay hình chữ nhật \(ADHE\) quanh \(AD\) ta được hình trụ có chiều cao \(AD\) và bán kính đáy \(HD\).
Nên ${S_{xq}} = 2.\pi HD.AD = \dfrac{{3456}}{{25}}\pi \left( {c{m^2}} \right)$
Một thùng nước có dạng hình trụ với chiều cao 1,6m và bán kính đáy 0,5m. Người ta sơn toàn bộ phía ngoài mặt xung quanh mặt xung quanh của thùng nước này (trừ hai mặt đáy) (lấy \(\pi \approx 3,14\)).
Diện tích bề mặt được sơn của thùng nước là:
\(m^2\).
Diện tích bề mặt được sơn của thùng nước là:
\(m^2\).
Thùng nước hình trụ có chiều cao \(h = 1,6m\) và bán kính đáy \(R = 0,5m\).
Diện tích bề mặt được sơn của thùng nước là:
\(2\pi Rh = 2.3,14.0,5.1,6 = 5,024\,\,\,\,\left( {{m^2}} \right)\)
Vậy diện tích bề mặt được sơn của thùng nước là \(5,024\,{m^2}\).

