Câu hỏi:
2 năm trước
Cho tam giác $ABC(AB < AC)$ nội tiếp đường tròn $\left( {O;R} \right)$ đường kính $BC.$ Vẽ đường cao $AH$ của tam giác ${\rm{ABC}}{\rm{.}}$ Đường tròn tâm $K$ đường kính $AH$ cắt $AB,AC$ lần lượt tại $D$ và $E.$
Chọn khẳng định sai.
Trả lời bởi giáo viên
Đáp án đúng: d
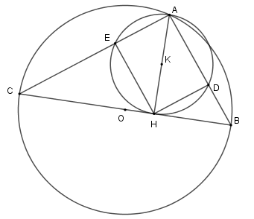
Xét \(\left( O \right)\) có $\widehat {CAD} = 90^\circ $ (góc nội tiếp chắn nửa đường tròn)
Xét \(\left( K \right)\) có \(\widehat {AEH} = \widehat {ADH} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Nên tứ giác $ADHE$ là hình chữ nhật ( vì có ba góc vuông)\( \Rightarrow \) phương án A đúng.
Xét tam giác vuông \(AHB\) có \(A{H^2} = AD.AB \Rightarrow \) phương án C đúng
Xét tam giác vuông \(A{H^2} = AC.AE\) nên \(AD.AB = AC.AE \Rightarrow \) phương án B đúng
Hướng dẫn giải:
Sử dụng dấu hiệu nhận biết hình chữ nhật và hệ thức lượng trong tam giác vuông
