Cho \(\alpha \) là góc nhọn bất kỳ. Khi đó \(C={\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha {\cos ^2}\alpha \) bằng
Ta có \({\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha .1\)
\( = {\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha .{\cos ^2}\alpha .\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)\) (vì \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\))
\( = {\left( {{{\sin }^2}\alpha } \right)^3} + 3{\left( {{{\sin }^2}\alpha } \right)^2}.{\cos ^2}\alpha + 3{\sin ^2}\alpha .{\left( {{{\cos }^2}\alpha } \right)^2} + {\left( {{{\cos }^2}\alpha } \right)^3}\)
\( = {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)^3} = 1\) (vì \({\sin ^2}\alpha + {\cos ^2}\alpha = 1)\)
Cho \(\alpha \) là góc nhọn bất kỳ. Cho \(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \), chọn kết luận đúng.
Với \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};{\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha ,\,{\cos ^2}\alpha = 1 - {\sin ^2}\alpha .\)
\(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \)\( = {\cos ^2}\alpha .\dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + {\sin ^2}\alpha .\dfrac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = {\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Vậy \(P = 1.\)
Cho \(\alpha \) là góc nhọn bất kỳ. Biểu thức \(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\) bằng
Với \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\) ta có
\(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\)\( = \dfrac{{{{\cos }^2}\alpha }}{{\sin \alpha .\cos \alpha }} - \dfrac{{{{\sin }^2}\alpha }}{{\sin \alpha .\cos \alpha }} = \dfrac{{\cos \alpha }}{{\sin \alpha }} - \dfrac{{\sin \alpha }}{{\cos \alpha }} = \cot \alpha - \tan \alpha \)
Vậy \(Q = \cot \alpha - \tan \alpha \).
Cho \(\tan \alpha = 4\). Tính giá trị của biểu thức \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)
Vì \(\tan \alpha = 4\) nên \(\cos \alpha \ne 0\), chia cả tử và mẫu của \(P\) cho \(\cos \alpha \) ta được
Ta có \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)\( = \dfrac{{3.\dfrac{{\sin \alpha }}{{\cos \alpha }} - 5\dfrac{{\cos \alpha }}{{\cos \alpha }}}}{{4\dfrac{{\cos \alpha }}{{\cos \alpha }} + \dfrac{{\sin \alpha }}{{\cos \alpha }}}}\)\( = \dfrac{{3.\tan \alpha - 5}}{{4 + \tan \alpha }}\)
Thay \(\tan \alpha = 4\) ta được \(P = \dfrac{{3.4 - 5}}{{4 + 4}} = \dfrac{7}{8}\).
Vậy \(P = \dfrac{7}{8}\).
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
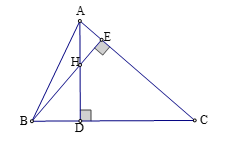
Xét tam giác vuông \(ABD\) và \(ADC\), ta có: \(\tan B = \dfrac{{AD}}{{BD}};tanC = \dfrac{{AD}}{{CD}}\).
Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\) (1)
Lại có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) và \(\widehat {HDB} = \widehat {ADC} = {90^0}\).
Do đó \(\Delta BDH \sim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\) (2).
Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\) (3).
Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{3}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{3}{{2 + 3}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{3}{5}\), suy ra \(AD = \dfrac{5}{3}HD\).
Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{\dfrac{5}{3}HD}}{{DH}} = \dfrac{5}{3}.\)
Tính các giá trị lượng giác còn lại của góc \(\alpha \) biết \(\sin \alpha = \dfrac{3}{5}\).
Ta có \(\sin \alpha = \dfrac{3}{5}\) suy ra \({\sin ^2}\alpha = \dfrac{9}{{25}}\), mà \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), do đó \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - \dfrac{9}{{25}} = \dfrac{{16}}{{25}}\), suy ra \(\cos \alpha = \dfrac{4}{5}\).
Do đó \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }} = \dfrac{3}{5}:\dfrac{4}{5} = \dfrac{3}{5}.\dfrac{5}{4} = \dfrac{3}{4}\)
\(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{4}{5}:\dfrac{3}{5} = \dfrac{4}{5}.\dfrac{5}{3} = \dfrac{4}{3}\).
Vậy \(\cos \alpha = \dfrac{4}{5},\tan \alpha = \dfrac{3}{4},\cot \alpha = \dfrac{4}{3}.\)
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
Cho $\alpha $ là góc nhọn bất kỳ, khi đó ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
Cho $\alpha $ là góc nhọn bất kỳ, khi đó
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1\)
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};$
$1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }};$
$1 + {\cot ^2}\alpha = \dfrac{1}{{{{\sin }^2}\alpha }}.$
Cho $\alpha $ và $\beta $ là hai góc nhọn bất kỳ thỏa mãn $\alpha + \beta = 90^\circ $. Khẳng định nào sau đây là đúng?
Với hai góc \(\alpha ,\beta \) mà \(\alpha + \beta = {90^0}\).
Ta có: \(\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\)
\(\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta \).
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
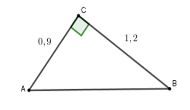
Theo định lý Py-ta-go ta có: $A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {0,{9^2} + 1,{2^2}} = 1,5$
Xét tam giác $ABC$ vuông tại $C$ có $\sin B = \dfrac{{AC}}{{AB}} = \dfrac{{0,9}}{{1,5}} = \dfrac{3}{5} = 0,6$ và $\cos B = \dfrac{{BC}}{{AB}} = \dfrac{{1,2}}{{1,5}} = \dfrac{4}{5} = 0,8$
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
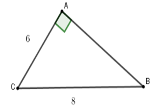
Theo định lý Py-ta-go ta có: $B{C^2} = A{C^2} + A{B^2} \Rightarrow AB = \sqrt {{8^2} - {6^2}} \approx 5,29$
Xét tam giác $ABC$ vuông tại $C$ có $\tan C = \dfrac{{AB}}{{AC}} \approx \dfrac{{5,29}}{6} \approx 0,88.$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(AB = 13\,cm,\,BH = 0,5\,dm\) Tính tỉ số lượng giác $\sin C$ (làm tròn đến chữ số thập phân thứ $2$ )
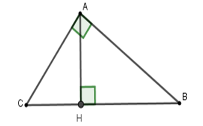
Đổi $0,5\,dm = 5\,cm$
Xét tam giác $ABC$ vuông tại $A$,
theo hệ thức lượng trong tam giác vuông ta có
$A{B^2} = BH.BC \Rightarrow BC = \dfrac{{A{B^2}}}{{BH}} = \dfrac{{{{13}^2}}}{5} = 33,8\,\,cm$
$ \Rightarrow \sin C = \dfrac{{AB}}{{BC}}$
$= \dfrac{{13}}{{33,8}} \approx 0,38$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
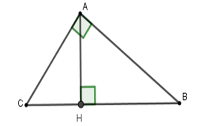
Xét tam giác $ABC$ vuông tại $A$ có $BC = BH + CH = 7\,\,cm$
theo hệ thức lượng trong tam giác vuông ta có $A{C^2} = CH.BC \Rightarrow A{C^2} = 4.7 \Rightarrow AC \approx 5,29\,\,cm$
$ \Rightarrow \cos C = \dfrac{{AC}}{{BC}} = \dfrac{{5,29}}{7} \approx 0,76$.
Cho tam giác $ABC$ vuông tại $A$. Hãy tính $\tan C$ biết rằng \(\cot B = 2\).
Vì tam giác $ABC$ vuông tại $A$ nên $\widehat B + \widehat C = 90^\circ $$ \Rightarrow \tan C = \cot B = 2$
Cho tam giác $ABC$ vuông tại $A$ có \(AB = 5\,cm,\,\,\cot C = \dfrac{7}{8}\) . Tính độ dài các đoạn thẳng $AC$ và $BC$ . (làm tròn đến chữ số thập phân thứ $2$ )
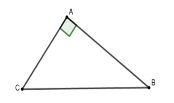
Vì tam giác $ABC$ vuông tại $A$ nên $\cot C = \dfrac{{AC}}{{AB}} \Rightarrow AC = AB.\cot C = 5.\dfrac{7}{8} = \dfrac{{35}}{8} \approx 4,38\,\,cm$
Theo định lý Pytago ta có \(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{35}}{8}} \right)^2} \Rightarrow BC \approx 6,64\)
Vậy $AC \approx 4,38(cm);BC \approx 6,64(cm)$.
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
Ta có ${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - \dfrac{4}{{25}} = \dfrac{{21}}{{25}}$
$\Rightarrow \sin \alpha = \dfrac{\sqrt {21}}{5}$
Lại có $\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{\dfrac{2}{5}}}{{\dfrac{{\sqrt {21} }}{5}}} = \dfrac{2}{{\sqrt {21} }}$.
Vậy $\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{2}{{\sqrt {21} }}$.
Không dùng bảng số và máy tính, hãy so sánh \(\sin 20^\circ \) và \(\sin 70^\circ \)
Vì $20^\circ < 70^\circ \Leftrightarrow \sin 20^\circ < \sin 70^\circ $.
Sắp xếp các tỉ số lượng giác \(\tan 43^\circ ,\,\,\cot 71^\circ ,\,\,\tan 38^\circ ,\,\,\cot 69^\circ 15',\,\tan 28^\circ \) theo thứ tự tăng dần.
Ta có $\cot 71^\circ = \tan 19^\circ \,$ vì $71^\circ + 19^\circ = 90^\circ $; $\cot 69^\circ 15' = \tan 20^\circ 45'$ vì $69^\circ 15' + 20^\circ 45' = 90^\circ $
Mà $ 19^\circ <20^\circ 45' < 28^\circ < 38^\circ < 43^\circ $ nên $ \tan 19^\circ < \tan 20^\circ 45' <\tan 28^\circ < \tan 38^\circ < \tan 43^\circ $
$ \Leftrightarrow \cot 71^\circ <\cot 69^\circ 15' < \tan 28^\circ < \tan 38^\circ < \tan 43^\circ $
Tính giá trị biểu thức $A = {\sin ^2}1^\circ + {\sin ^2}2^\circ + ... + {\sin ^2}88^\circ + {\sin ^2}89^\circ + {\sin ^2}90^\circ $
Ta có ${\sin ^2}89^\circ = {\cos ^2}1^\circ ;{\sin ^2}88^\circ = {\cos ^2}2^\circ ;...;{\sin ^2}46^\circ = {\cos ^2}44^\circ $ và ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
Nên $A = \left( {{{\sin }^2}1^\circ + {{\sin }^2}89^\circ } \right) + \left( {{{\sin }^2}2^\circ + {{\sin }^2}88^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\sin }^2}46^\circ } \right) + {\sin ^2}45^\circ + {\sin ^2}90^\circ $
$ = \left( {{{\sin }^2}1^\circ + {{\cos }^2}1^\circ } \right) + \left( {{{\sin }^2}2^\circ + {{\cos }^2}2^\circ } \right) + ... + \left( {{{\sin }^2}44^\circ + {{\cos }^2}44^\circ } \right) + {\sin ^2}45^\circ + {\sin ^2}90^\circ $
$ = \underbrace {1 + 1 + ... + 1}_{44\,\,so\,1} + \dfrac{1}{2} + 1$$ = 44.1 + \dfrac{3}{2} = \dfrac{{91}}{2}$.
Vậy $A = \dfrac{{91}}{2}.$
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
Ta có $C = {\sin ^4}\alpha + {\cos ^4}\alpha = {\sin ^4}\alpha + {\cos ^4}\alpha + 2{\sin ^2}\alpha .{\cos ^2}\alpha - 2{\sin ^2}\alpha .{\cos ^2}\alpha $
$ = {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right)^2} - 2{\sin ^2}\alpha .{\cos ^2}\alpha = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $ (vì ${\sin ^2}\alpha + {\cos ^2}\alpha = 1$)
Vậy $C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $.

