Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng

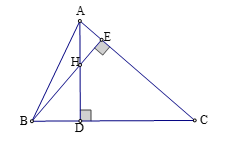
Xét tam giác vuông \(ABD\) và \(ADC\), ta có: \(\tan B = \dfrac{{AD}}{{BD}};tanC = \dfrac{{AD}}{{CD}}\).

Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\)   (1)

Lại có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) và \(\widehat {HDB} = \widehat {ADC} = {90^0}\).

Do đó \(\Delta BDH \sim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\)  (2).

Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\)  (3).

Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{3}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{3}{{2 + 3}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{3}{5}\), suy ra \(AD = \dfrac{5}{3}HD\).

Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{\dfrac{5}{3}HD}}{{DH}} = \dfrac{5}{3}.\)