Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
Với $\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};{\sin ^2}\alpha + {\cos ^2}\alpha = 1$.
$A = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $$ = {\cot ^2}\alpha - {\sin ^2}\alpha .{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $
$ = 1 - {\sin ^2}\alpha .\dfrac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = 1 - {\cos ^2}\alpha = {\sin ^2}\alpha $
Vậy $P = {\sin ^2}\alpha $.
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
Với $\tan \alpha = \dfrac{{sin\alpha }}{{\cos \alpha }};{\cos ^2}\alpha = 1 - {\sin ^2}\alpha $.
$Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$$ = \dfrac{{1 - {{\sin }^2}\alpha + 2{{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} = \dfrac{{1 - {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }} + \dfrac{{2{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}$
$ = 1 + 2.{\left( {\dfrac{{\sin \alpha }}{{\cos \alpha }}} \right)^2} = 1 + 2{\tan ^2}\alpha $
Vậy $Q = 1 + 2{\tan ^2}\alpha $.
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
Vì $\tan \alpha = 2$ nên $\cos \alpha \ne 0$
Ta có $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$$ = \dfrac{{2\dfrac{{\sin \alpha }}{{\cos \alpha }} + \dfrac{{\cos \alpha }}{{\cos \alpha }}}}{{\dfrac{{\cos \alpha }}{{\cos \alpha }} - 3.\dfrac{{\sin \alpha }}{{\cos \alpha }}}}$$ = \dfrac{{2.\tan \alpha + 1}}{{1 - 3\tan \alpha }}$
Thay $\tan \alpha = 2$ ta được $G = \dfrac{{2.2 + 1}}{{1 - 3.2}} = - \dfrac{5}{5}=-1$.
Vậy $G = - 1$.
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
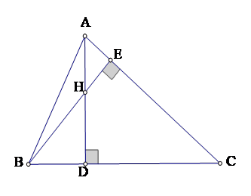
Xét tam giác vuông $ABD$ và $ADC$, ta có: \(\tan B = \dfrac{{AD}}{{BD}};tanC = \dfrac{{AD}}{{CD}}\).
Suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{BD.CD}}\) (1)
Lại có \(\widehat {HBD} = \widehat {CAD}\) (cùng phụ với \(\widehat {ACB}\)) và \(\widehat {HDB} = \widehat {ADC} = {90^0}\).
Do đó \(\Delta BDH \backsim \Delta ADC\) (g.g), suy ra \(\dfrac{{DH}}{{DC}} = \dfrac{{BD}}{{AD}}\), do đó \(BD.DC = DH.AD\) (2).
Từ (1) và (2) suy ra \(\tan B.\tan C = \dfrac{{A{D^2}}}{{DH.AD}} = \dfrac{{AD}}{{DH}}\) (3).
Theo giả thiết \(\dfrac{{HD}}{{AH}} = \dfrac{1}{2}\) suy ra \(\dfrac{{HD}}{{AH + HD}} = \dfrac{1}{{2 + 1}}\) hay \(\dfrac{{HD}}{{AD}} = \dfrac{1}{3}\), suy ra \(AD = 3HD\).
Thay vào (3) ta được: \(\tan B.\tan C = \dfrac{{3HD}}{{DH}} = 3\).
Cho $ \alpha $ là góc nhọn. Tính \(\cot \alpha \) biết \(\sin \alpha = \dfrac{5}{{13}}\).
Ta có \(\sin \alpha = \dfrac{5}{{13}}\) suy ra \({\sin ^2}\alpha = \dfrac{{25}}{{169}}\), mà \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), do đó \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - \dfrac{{25}}{{169}} = \dfrac{{144}}{{169}}\)
Suy ra \(\cos \alpha = \dfrac{{12}}{{13}}\).
Do đó \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }} = \dfrac{{12}}{{13}}:\dfrac{5}{{13}} = \dfrac{{12}}{{13}}.\dfrac{{13}}{5} = \dfrac{{12}}{5}\).
Tính giá trị biểu thức $B = \tan 1^\circ .\tan 2^\circ .\tan 3^\circ .....\tan88^\circ .\tan89^\circ $
Ta có $\tan 89^\circ = \cot1^\circ ;\tan 88^\circ = \cot2^\circ ;..;\tan 46^\circ = \cot44^\circ $ và $\tan \alpha .\cot\alpha = 1$
Nên $B = \left( {\tan 1^\circ .\tan 89^\circ } \right).\left( {\tan 2^\circ .\tan 88^\circ } \right)....\left( {\tan 46^\circ .\tan 44^\circ } \right).\tan 45^\circ $
$ = \left( {\tan 1^\circ .\cot 1^\circ } \right).\left( {\tan 2^\circ .\cot 2^\circ } \right).\left( {\tan 3^\circ .\cot 3^\circ } \right)....\left( {\tan 44^\circ .\cot 44^\circ } \right).\tan 45^\circ $
$ = 1.1.1....1.1 = 1$
Vậy $B = 1$.
Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\) biết \(\tan \alpha = 3.\)
Vì \(\tan \alpha = 3 \ne 0 \Rightarrow \cos \alpha \ne 0.\) Chia cả tử và mẫu của \(B\) cho \({\cos ^2}\alpha \) ta được
\(B = \dfrac{{\dfrac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} - 3\dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}}{{\dfrac{3}{{{{\cos }^2}\alpha }} - \dfrac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }}}} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3.\dfrac{1}{{{{\cos }^2}\alpha }} - {{\tan }^2}\alpha }}\)
\( = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3\left( {1 + {{\tan }^2}\alpha } \right) - {{\tan }^2}\alpha }} = \dfrac{{1 - 3{{\tan }^2}\alpha }}{{3 + 2{{\tan }^2}\alpha }}\)
\( = \dfrac{{1 - 3.9}}{{3 + 2.9}} = - \dfrac{{26}}{{21}}\)
Hay \(B = - \dfrac{{26}}{{21}} < 0\)
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
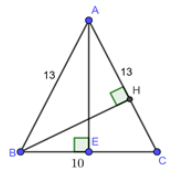
Vì tam giác \(ABC\) cân tại\(A\) nên là \(AE\) đường cao đồng thời là đường trung tuyến
\( \Rightarrow E\) là trung điểm \(BC \Rightarrow EB = EC = 5\)
Xét \(\Delta ABE\) vuông tại \(E\) có:
\(A{E^2} + E{B^2} = A{B^2}\) (Định lý Py-ta-go)
\(A{E^2} + {5^2} = {13^2} \Rightarrow AE = 12\)
\( \Rightarrow {S_{ABC}} = \dfrac{{AE.BC}}{2} = \dfrac{{12.10}}{2} = 60\)
Mặt khác: \({S_{ABC}} = \dfrac{{AC.BH}}{2} \Leftrightarrow 60 = \dfrac{{13.BH}}{2}\)\( \Rightarrow BH = \dfrac{{120}}{{13}}\)
Xét \(\Delta ABH\) vuông tại \(H\) có: \(sinA = \dfrac{{BH}}{{BA}} = \dfrac{{120}}{{13}}:13 = \dfrac{{120}}{{169}}.\)
Tính diện tích hình bình hành \(ABCD\) biết \(AD = 12cm;DC = 15cm;\angle ADC = {70^0}\).
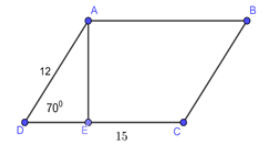
Xét \(\Delta ADE\) vuông tại \(E\) có:
\(sinD = \dfrac{{AE}}{{AD}} \Leftrightarrow sin{70^0} = \dfrac{{AE}}{{12}} \Rightarrow AE = 12.sin{70^0}\)
\( \Rightarrow {S_{ABCD}} = AE.DC = 12.\sin {70^0}.15 \approx 169,1\,cm^2\)
Tính số đo góc nhọn \(\alpha \) biết \(10{\sin ^2}\alpha + 6{\cos ^2}\alpha = 8\).
Ta có: \(10{\sin ^2}\alpha + 6{\cos ^2}\alpha = 8\)
\(\begin{array}{l} \Leftrightarrow 4{\sin ^2}\alpha + 6\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = 8\\ \Leftrightarrow 4{\sin ^2}\alpha + 6 = 8\\ \Leftrightarrow {\sin ^2}\alpha = \dfrac{1}{2} \Leftrightarrow \sin \alpha = \pm \dfrac{{\sqrt 2 }}{2}\end{array}\)
\(Do\,\,\alpha < {90^0} \Rightarrow \sin \alpha > 0 \Leftrightarrow \sin \alpha = \dfrac{{\sqrt 2 }}{2}.\)
Vậy \(\alpha = {45^0}.\)
Tính giá trị của các biểu thức sau:
\(A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}{55^0} + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
\(\,\,A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\)
Ta có:
\(\begin{array}{l}A = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\sin ^2}55 + {\sin ^2}{65^0} + {\sin ^2}{75^0}\\\,\,\,\,\, = {\sin ^2}{15^0} + {\sin ^2}{25^0} + {\sin ^2}{35^0} + {\sin ^2}{45^0} + {\cos ^2}{35^0} + {\cos ^2}{25^0} + {\cos ^2}{15^0}\\\,\,\,\,\, = \left( {{{\sin }^2}{{15}^0} + {{\cos }^2}{{15}^0}} \right) + \left( {{{\sin }^2}{{25}^0} + {{\cos }^2}25} \right) + \left( {{{\sin }^2}{{35}^0} + {{\cos }^2}{{35}^0}} \right) + {\sin ^2}{45^0}\\\,\,\,\, = 1 + 1 + 1 + {\left( {\dfrac{{\sqrt 2 }}{2}} \right)^2} = 3 + \dfrac{1}{2} = \dfrac{7}{2}.\end{array}\)
Tính giá trị của các biểu thức sau:
\(B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)
\(\,\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}.\)
Ta có:
\(\begin{array}{l}\,B = \tan {10^0}.\tan {80^0} - \tan {20^0}.\tan {70^0}\\\,\,\,\,\, = \tan {10^0}.\cot{10^0} - \tan {20^0}.\cot {20^0}\\\,\,\,\,\, = 1 - 1 = 0.\end{array}\)
Biết \({0^0} < \alpha < {90^0}\). Giá trị bủa biểu thức \(\left[ {\sin \alpha + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha - 2\cos \left( {{{90}^0} - \alpha } \right)} \right]\) bằng:
\(\begin{array}{l}\left[ {\sin \alpha + 3\,\cos \left( {{{90}^0} - \alpha } \right)} \right]:\left[ {\sin \alpha - 2\cos \left( {{{90}^0} - \alpha } \right)} \right] \\= \left( {\sin \alpha + 3\sin \alpha } \right):\left( {\sin \alpha - 2\sin \alpha } \right)\\ = \left( {4\sin \alpha } \right):\left( { - \sin \alpha } \right) \\= - 4.\end{array}\)
Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).
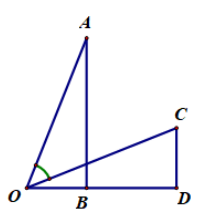
Xét \(\Delta OAB\) và \(\Delta COD\) có:
\(\begin{array}{l}\angle OBA = \angle CDO = {90^o}\,\,\,\,\left( {gt} \right)\\OB = CD\,\,\,\left( {gt} \right)\\AB = OD\,\,\,\,\left( {gt} \right)\\ \Rightarrow \Delta OAB = \Delta COD\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow OA = OC\) (2 cạnh tương ứng)
\( \Rightarrow OA.OC = O{A^2} = O{B^2} + A{B^2} = {a^2} + {b^2}\) (Định lý Pytago)
\(\begin{array}{l}\cos \angle AOC = \cos \left( {\angle AOB - \angle COD} \right) = \cos \angle AOB\cos \angle COD + \sin \angle AOB\sin \angle COD\\ = \dfrac{{OB}}{{OA}}.\dfrac{{OD}}{{OC}} + \dfrac{{AB}}{{OA}}.\dfrac{{CD}}{{OC}} = \dfrac{{OB.OD + AB.CD}}{{OA.OC}} = \dfrac{{ab + ab}}{{{a^2} + {b^2}}} = \dfrac{{2ab}}{{{a^2} + {b^2}}}.\end{array}\)
Cho tam giác \(ABC\) có \(\angle B,\angle C\) là góc nhọn và có diện tích không đổi. Tìm giá trị nhỏ nhất của biểu thức \(P = 2B{C^2} + A{C^2} + A{B^2}\).
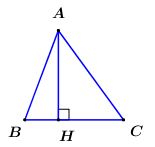
Kẻ đường cao \(AH\). Vì \(\angle B,\,\,\angle C\) là các góc nhọn nên \(H\) thuộc đoạn thẳng \(BC\).
Áp dụng định lí Pytago ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\A{B^2} = A{H^2} + B{H^2}\end{array}\)
\( \Rightarrow P = 2B{C^2} + 2A{H^2} + B{H^2} + H{C^2}\).
Ta có \(B{C^2} + A{H^2} \ge 2BC.AH = 4{S_{\Delta ABC}}\).
\(B{H^2} + C{H^2} \ge \dfrac{{{{\left( {BH + CH} \right)}^2}}}{2} = \dfrac{{B{C^2}}}{2}\).
Do đó \(P \ge 8{S_{\Delta ABC}} + \dfrac{{B{C^2}}}{2}\).
Do \({S_{\Delta ABC}}\) không đổi, \(A,\,\,B,\,\,C\) cố định nên \(P\) đạt giá trị nhỏ nhất bằng \(8{S_{\Delta ABC}} + \dfrac{{B{C^2}}}{2}\).
Dấu “=” xảy ra khi \(BH = CH \Rightarrow \Delta ABC\) cân tại \(A\).

