Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
Trả lời bởi giáo viên
Đáp án đúng: a
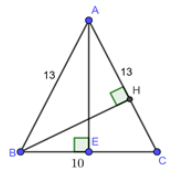
Vì tam giác \(ABC\) cân tại\(A\) nên là \(AE\) đường cao đồng thời là đường trung tuyến
\( \Rightarrow E\) là trung điểm \(BC \Rightarrow EB = EC = 5\)
Xét \(\Delta ABE\) vuông tại \(E\) có:
\(A{E^2} + E{B^2} = A{B^2}\) (Định lý Py-ta-go)
\(A{E^2} + {5^2} = {13^2} \Rightarrow AE = 12\)
\( \Rightarrow {S_{ABC}} = \dfrac{{AE.BC}}{2} = \dfrac{{12.10}}{2} = 60\)
Mặt khác: \({S_{ABC}} = \dfrac{{AC.BH}}{2} \Leftrightarrow 60 = \dfrac{{13.BH}}{2}\)\( \Rightarrow BH = \dfrac{{120}}{{13}}\)
Xét \(\Delta ABH\) vuông tại \(H\) có: \(sinA = \dfrac{{BH}}{{BA}} = \dfrac{{120}}{{13}}:13 = \dfrac{{120}}{{169}}.\)
Hướng dẫn giải:
Sử dụng định nghĩa tỉ số lượng giác
Tính chất tam giác cân.
Công thức tính diện tích tam giác
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
