Câu hỏi:
2 năm trước
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
Trả lời bởi giáo viên
Đáp án đúng: a
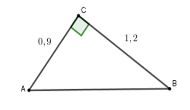
Theo định lý Py-ta-go ta có: $A{B^2} = A{C^2} + B{C^2} \Rightarrow AB = \sqrt {0,{9^2} + 1,{2^2}} = 1,5$
Xét tam giác $ABC$ vuông tại $C$ có $\sin B = \dfrac{{AC}}{{AB}} = \dfrac{{0,9}}{{1,5}} = \dfrac{3}{5} = 0,6$ và $\cos B = \dfrac{{BC}}{{AB}} = \dfrac{{1,2}}{{1,5}} = \dfrac{4}{5} = 0,8$
Hướng dẫn giải:
Bước 1: Tính cạnh còn lại theo định lý Pytago
Bước 2: Sử dụng định nghĩa tỉ số lượng giác của góc nhọn


