Trả lời bởi giáo viên
Đáp án đúng: c
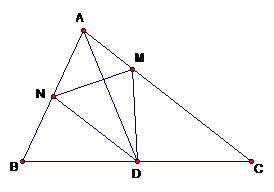
Nhận thấy hai tam giác \(ADC\) và \(ABC\) có chung chiều cao hạ từ đỉnh \(A\)
Mà \(BD = \dfrac{1}{2} \times BC\) nên \({S_{{\rm{ADC}}}} = \dfrac{1}{2}{S_{ABC}}{\rm{ }}\)
Nhận thấy hai tam giác \(ADM\) và \(ADC\) có chung chiều cao hạ từ đỉnh \(D\) mà \(AM = \dfrac{1}{3} \times AC\) nên \({{\rm{S}}_{{\rm{ADM}}}} = \dfrac{1}{3} \times {\rm{ }}{{\rm{S}}_{{\rm{ADC}}}}\).
Do đó: \({S_{ADM}} = \dfrac{1}{3} \times {S_{ADC}}\)\( = \dfrac{1}{3} \times \dfrac{1}{2} \times {S_{ABC}} = \dfrac{1}{6} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}}\)
Vậy \({S_{ADM}} = \dfrac{1}{6} \times {S_{ABC}}\)
Hướng dẫn giải:
Diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
Tìm quan hệ về diện tích giữa hai tam giác \(ADC\) và \(ABC\).
Tìm quan hệ về diện tích giữa hai tam giác \(ADM\) và \(ADC\).
Từ đó suy ra quan hệ về diện tích giữa hai tam giác \(ADM\) và \(ABC\).
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
