Một hình tròn có chu vi bằng 18,84cm. Diện tích hình tròn đó là:
Bán kính hình tròn bằng: \(18,84:2:3,4 = 3\,cm\)
Diện tích hình tròn là: \(3 \times 3 \times 3,14 = 28,26\,c{m^2}\)
Nghiệm của phương trình \(2x - 5 = 0\) là:
Ta có: \(2x - 5 = 0 \Leftrightarrow 2x = 5\, \Leftrightarrow x = \dfrac{5}{2}\).
Số tiếp theo của dãy số: 1 ; 3 ; 4 ; 7 ; 11 ; 18 ; ……
Ta thấy
\(\begin{array}{l}1 + 3 = 4\\3 + 4 = 7\\4 + 7 = 11\\7 + 11 = 18\end{array}\)
Hay kể từ số hạng thứ ba thì tổng hai số hạng liền trước bằng số hạng tiếp theo.
Từ đó ta có số cần điền là \(11 + 18 = 29\)
Có bao nhiêu giá trị của \(x\) thỏa mãn phương trình \(\left| {x - 3} \right| = 1 - 3x\).
\(\left| {x - 3} \right| = 1 - 3x \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 3 \ge 0\\x - 3 = 1 - 3x\end{array} \right.\\\left\{ \begin{array}{l}x - 3 < 0\\x - 3 = 3x - 1\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 3\\x + 3x = 1 + 3\end{array} \right.\\\left\{ \begin{array}{l}x < 3\\x - 3x = 3 - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 3\\x = 1\end{array} \right.\\\left\{ \begin{array}{l}x < 3\\x = - 1\end{array} \right.\end{array} \right. \Leftrightarrow x = - 1\).
Vậy có 1 giá trị \(x\) thỏa mãn là \(x = - 1.\)
Tập nghiệm của bất phương trình \(5x + 1 < - 3\) là:
\(5x + 1 < - 3 \Leftrightarrow 5x < - 3 - 1\) \( \Leftrightarrow x < \dfrac{{ - 4}}{5}\).
Tập nghiệm của bất phương trình là \(S = \left\{ {x|x < - \dfrac{4}{5}} \right\}\).
Cho tập hợp \(B = \left\{ {a;b;c;1;2} \right\}\). Số tập con gồm hai phần tử của tập hợp \(B\) là:
Các tập hợp gồm hai phần tử thuộc tập hợp \(B\) là: \(\left\{ {a;b} \right\},\left\{ {a;c} \right\},\left\{ {a;1} \right\},\left\{ {a;2} \right\},\)\(\left\{ {b;c} \right\},\left\{ {b;1} \right\},\left\{ {b;2} \right\},\)\(\left\{ {c;1} \right\},\left\{ {c;2} \right\},\left\{ {1;2} \right\}\)
Vậy có 10 tập hợp thỏa mãn đề bài.
Qua 5 điểm phân biệt (không có ba điểm nào thẳng hàng), ta vẽ được bao nhiêu đường thẳng?
Gọi 5 điểm đó là $A,B,C,D,E.$
Vì qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên các đường thẳng tạo thành từ 5 điểm trên là: \(AB,AC,AD,AE,BC,BD,BE,\)\(CD,CE,DE.\)
Vậy có 10 đường thẳng được tạo thành.
Chọn câu đúng. Giá trị của phân thức \(\dfrac{{{x^2} - x}}{{2(x - 1)}}\) tại \(x = 4\) là:
Đk: \(x - 1 \ne 0 \Leftrightarrow x \ne 1.\)
\(A = \dfrac{{{x^2} - x}}{{2(x - 1)}} = \dfrac{{x(x - 1)}}{{2(x - 1)}} = \dfrac{x}{2} (x \ne 1)\).
Với \(x = 4\) (tmđk) ta thay \(x = 4\) vào A ta được: \(A = \dfrac{4}{2} = 2.\)
Với điều kiện nào của \(x\) thì \(\dfrac{{x - 2}}{{3 + 2x}} \le 0\).
\(\dfrac{{x - 2}}{{3 + 2x}} \le 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 2 \ge 0\\3 + 2x < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 2 \le 0\\3 + 2x > 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 2 \ge 0\\3 + 2x < 0\end{array} \right.\\\left\{ \begin{array}{l}x - 2 \le 0\\3 + 2x > 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 2\\x < \dfrac{{ - 3}}{2}\end{array} \right.\\\left\{ \begin{array}{l}x \le 2\\x > \dfrac{{ - 3}}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \dfrac{{ - 3}}{2} < x \le 2\).
Vậy \( - \dfrac{3}{2} < x \le 2.\)
Tính nhanh \(3 + \dfrac{4}{9} \times \dfrac{7}{{25}} \times \dfrac{{27}}{{12}} \times {\rm{ 3}}\dfrac{{\rm{4}}}{{\rm{7}}} - \dfrac{7}{{25}}\)
Ta có:
\(\begin{array}{l}3 + \dfrac{4}{9}\times \dfrac{7}{{25}}\times \dfrac{{27}}{{12}}\times {\rm{ 3}}\dfrac{{\rm{4}}}{{\rm{7}}} - \dfrac{7}{{25}}\\ = 3 + \dfrac{4}{9}\times \dfrac{7}{{25}}\times \dfrac{9}{4}\times {\rm{ }}\dfrac{{{\rm{25}}}}{{\rm{7}}} - \dfrac{7}{{25}}\\ = 3 + 1 - \dfrac{7}{{25}}\\ = 4 - \dfrac{7}{{25}}\\ = \dfrac{{93}}{{25}}\end{array}\)
Cho \(\Delta ABC\), đường phân giác góc \(B\) cắt \(AC\) tại \(D\) và cho biết \(AB = 10{\rm{ }}cm,{\rm{ }}BC = 15{\rm{ }}cm,\)\(AD = 6{\rm{ }}cm.\) Tính \(AC.\)
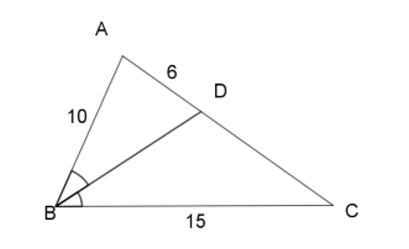
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: \(\dfrac{{BA}}{{AD}} = \dfrac{{BC}}{{CD}}\)
\( \Rightarrow \dfrac{{10}}{6} = \dfrac{{15}}{{CD}} \Leftrightarrow CD = \dfrac{{6.15}}{{10}} = 9\;cm\)
\( \Rightarrow AC = AD + DC = 6 + 9 = 15\;cm\).
Hình thang \(ABCD\) có đáy \(CD\) gấp đôi đáy \(AB\) và diện tích tam giác \(ACD\) là \(30\,c{m^2}\). Diện tích của hình thang \(ABCD\) là:
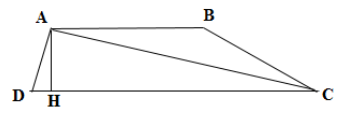
Kẻ đường cao \(AH\) của hình thang \(ABCD\).
Khi đó ta có: \({S_{ACD}} = \dfrac{1}{2}AH \times DC\) và \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right) \times AH}}{2}\).
Mà theo đề bài: \(CD = 2 \times AB\) nên ta có: \({S_{ACD}} = \dfrac{1}{2}AH \times 2AB\)\( = AH \times AB = 30c{m^2}\).
Suy ra: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right) \times AH}}{2}\)\( = \dfrac{{\left( {AB + 2AB} \right) \times AH}}{2} = \dfrac{{3AB \times AH}}{2}\)\( = \dfrac{{3 \times 30}}{2} = 45\,c{m^2}\).
Con hãy đọc bài sau và trả lời câu hỏi:
Những chiếc khăn quàng mùa đông
Một chú hươu cao cổ được đưa từ Châu Phi về vườn thú Thành Phố. Nó có tên là Bự. Bự rất thân thiện nên lúc nào các bạn nhỏ cũng xúm quanh chuồng của nó. Hôm nay, Bự bỗng nằm ủ rũ. Cậu bé Bi lo lắng hỏi Bự bị làm sao. Bự bảo:
- Mình bị viêm họng, Châu Phi quê mình quanh năm nóng. Còn Thành phố của bạn có mùa đông giá lạnh.
Bi nghĩ “phải giữ ấm cổ cho Bự” nên tháo ngay khăn len của mình choảng lên cổ Bự. Nhưng chiếc khăn quá nhỏ so với chiếc cổ dài của loài hươu. Thế là Bi chạy đi. Lát sau, Bi quay lại với hàng chục bạn nhỏ. Các bạn lần lượt tháo khăn trên cổ mình quàng cho hươu. Vậy là trên cổ Bự có bao nhiêu khăn len, khăn dạ. khăn bông với đủ mảu sắc xanh, đỏ, tím, vảng, ...
Các bạn nhỏ vuốt ve cái cổ dài rực rỡ sắc màu của Bự. Chú hươu cảm thấy cổ đỡ đau hẳn và mùa đông không còn lạnh lẽo nữa.
Theo Mai Hồng

Hươu cao cổ bị làm sao ?
c. Bị viêm họng
c. Bị viêm họng
c. Bị viêm họng
Hươu cao cổ bị viêm họng.
=> Đáp án: c
Cho tam giác \(ABC\) có \(AB = AC;{\rm{ }}BC = 8{\rm{ }}cm;\) \(BH\) và \(CK\) là hai đường trung tuyến kẻ từ \(B\) và \(C.\) Tính độ dài đoạn \(HK.\)
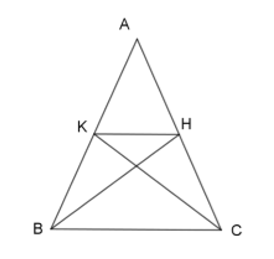
Theo bài ra ta có: \(AB = AC\) (1)
Ta lại có $BH$ và $CK$ là hai đường trung tuyến kẻ từ $B$ và $C$ của tam giác $ABC,$ suy ra $H$ và $K$ lần lượt là trung điểm của $AC$ và $AB.$
Khi đó, ta có:
\(AK = KB = \dfrac{1}{2}AB\;(2)\)
\(AH = HC = \dfrac{1}{2}AC\;(3)\)
Từ (1), (2) và (3) ta có: \(AK = AH\)
Vì $AK = AH$ và $AB = AC$ nên: \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\)
Xét \(\Delta AKH\) và \(\Delta ABC\) ta có:
+) \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\)
+) \(\widehat A\) chung
\( \Rightarrow \Delta AKH \backsim \Delta ABC\; (c - g - c)\)
\(\begin{array}{l} \Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{{KH}}{{BC}} = \dfrac{1}{2}\\ \Rightarrow \dfrac{{KH}}{8} = \dfrac{1}{2} \Leftrightarrow KH = \dfrac{8}{2} = 4\;cm\end{array}\).
Nếu bán kính một hình tròn tăng thêm \(20\% \) thì diện tích hình tròn tăng thêm \(56,54\,c{m^2}.\) Diện tích của hình tròn đó là:
\(56,54\,c{m^2}\) ứng với \(20\% \times 20\% = 0,44\)
Diện tích hình tròn đó là: \(56,54:0,44 = 128,5\,c{m^2}\)
Con hãy đọc bài sau và trả lời câu hỏi:
Những chiếc khăn quàng mùa đông
Một chú hươu cao cổ được đưa từ Châu Phi về vườn thú Thành Phố. Nó có tên là Bự. Bự rất thân thiện nên lúc nào các bạn nhỏ cũng xúm quanh chuồng của nó. Hôm nay, Bự bỗng nằm ủ rũ. Cậu bé Bi lo lắng hỏi Bự bị làm sao. Bự bảo:
- Mình bị viêm họng, Châu Phi quê mình quanh năm nóng. Còn Thành phố của bạn có mùa đông giá lạnh.
Bi nghĩ “phải giữ ấm cổ cho Bự” nên tháo ngay khăn len của mình choảng lên cổ Bự. Nhưng chiếc khăn quá nhỏ so với chiếc cổ dài của loài hươu. Thế là Bi chạy đi. Lát sau, Bi quay lại với hàng chục bạn nhỏ. Các bạn lần lượt tháo khăn trên cổ mình quàng cho hươu. Vậy là trên cổ Bự có bao nhiêu khăn len, khăn dạ. khăn bông với đủ mảu sắc xanh, đỏ, tím, vàng, ...
Các bạn nhỏ vuốt ve cái cổ dài rực rỡ sắc màu của Bự. Chú hươu cảm thấy cổ đỡ đau hẳn và mùa đông không còn lạnh lẽo nữa.
Theo Mai Hồng

Vì sao hươu cao cổ bị viêm họng ?
b. Vì nơi ở mới có mùa đông giá lạnh.
b. Vì nơi ở mới có mùa đông giá lạnh.
b. Vì nơi ở mới có mùa đông giá lạnh.
Hươu cao cổ bị viêm họng nơi ở mới có mùa đông giá lạnh.
=> Đáp án: b
Giải phương trình \(\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\) ta được tập nghiệm là:
ĐKXĐ: \(x \ne 2;\,\,x \ne - 2\)
\(\begin{array}{l}\,\,\,\,\,\,\,\dfrac{{x - 1}}{{x + 2}} - \dfrac{{1 - x}}{{2 - x}} = \dfrac{{2({x^2} + 2)}}{{{x^2} - 4}}\\ \Leftrightarrow \dfrac{{x - 1}}{{x + 2}} + \dfrac{{1 - x}}{{x - 2}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Leftrightarrow \dfrac{{(x - 1)(x - 2)}}{{(x - 2)(x + 2)}} + \dfrac{{(1 - x)(x + 2)}}{{(x - 2)(x + 2)}} = \dfrac{{2({x^2} + 2)}}{{(x - 2)(x + 2)}}\\ \Rightarrow (x - 1)(x - 2) + (1 - x)(x + 2) = 2({x^2} + 2)\\ \Leftrightarrow {x^2} - 2x - x + 2 + x + 2 - {x^2} - 2x = 2{x^2} + 4\\ \Leftrightarrow 2{x^2} + 4x = 0\\ \Leftrightarrow 2x(x + 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\,\,(TM)\\x = - 2\,\,\,\,\,(KTM)\end{array} \right.\end{array}\)
Vậy tập nghiệm của phương trình là \(S = \left\{ 0 \right\}.\)
Con hãy đọc bài sau và trả lời câu hỏi:
Những chiếc khăn quàng mùa đông
Một chú hươu cao cổ được đưa từ Châu Phi về vườn thú Thành Phố. Nó có tên là Bự. Bự rất thân thiện nên lúc nào các bạn nhỏ cũng xúm quanh chuồng của nó. Hôm nay, Bự bỗng nằm ủ rũ. Cậu bé Bi lo lắng hỏi Bự bị làm sao. Bự bảo:
- Mình bị viêm họng, Châu Phi quê mình quanh năm nóng. Còn Thành phố của bạn có mùa đông giá lạnh.
Bi nghĩ “phải giữ ấm cổ cho Bự” nên tháo ngay khăn len của mình choảng lên cổ Bự. Nhưng chiếc khăn quá nhỏ so với chiếc cổ dài của loài hươu. Thế là Bi chạy đi. Lát sau, Bi quay lại với hàng chục bạn nhỏ. Các bạn lần lượt tháo khăn trên cổ mình quàng cho hươu. Vậy là trên cổ Bự có bao nhiêu khăn len, khăn dạ. khăn bông với đủ mảu sắc xanh, đỏ, tím, vàng, ...
Các bạn nhỏ vuốt ve cái cổ dài rực rỡ sắc màu của Bự. Chú hươu cảm thấy cổ đỡ đau hẳn và mùa đông không còn lạnh lẽo nữa.
Theo Mai Hồng

Bi đã làm gì để giữ ấm cổ cho hươu ?
a. Tháo chiếc khăn len của mình choàng lên cổ Bự.
a. Tháo chiếc khăn len của mình choàng lên cổ Bự.
a. Tháo chiếc khăn len của mình choàng lên cổ Bự.
Bi đã tháo chiếc khăn len của mình choàng lên cổ để giữ ấm cổ cho Bự.
=> Đáp án: a
Để chuẩn bị cho năm học mới, bạn Nam đã mua tất cả \(26\) quyển vở gồm loại \(200\) trang và loại \(120\) trang. Mỗi quyển vở loại \(200\) trang có giá \(13500\) đồng, mỗi quyển vở loại \(120\) trang có giá \(9500\) đồng. Bạn Nam đã trả số tiền là \(263000\) đồng.
Tính số vở loại \(120\) trang mà bạn Nam đã mua?
Gọi số quyển vở loại 200 trang bạn Nam mua là x (quyển, điều kiện \(x \in {\mathbb{N}^*},{\rm{ }}x < 26\) ) thì số quyển vở loại 120 trang là: \(26-x\) ( quyển)
Số tiền mua vở loại 200 trang là: \(13500x\) (đồng)
Số tiền mua vở loại 120 trang là: \(9500\left( {26 - x} \right)\) (đồng)
Vì bạn Nam đã trả tổng số tiền là \(263000\) đồng nên ta có phương trình \(13500x + 9500(26 - x) = 263000\)
\( \Leftrightarrow 13500x - 9500x = 263000 - 9500. 26\).
\( \Leftrightarrow 4000x = 16000\)\( \Leftrightarrow x = 4\) (thỏa mãn)
Vậy bạn Nam mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang.
Để chuẩn bị cho năm học mới, bạn Nam đã mua tất cả \(26\) quyển vở gồm loại \(200\) trang và loại \(120\) trang. Mỗi quyển vở loại \(200\) trang có giá \(13500\) đồng, mỗi quyển vở loại \(120\) trang có giá \(9500\) đồng. Bạn Nam đã trả số tiền là \(263000\) đồng.
Nhân dịp đầu năm học mới, nhà sách thực hiện chương trình giảm giá cho học sinh học sinh giỏi như sau: mỗi quyển loại 200 trang được giảm 5% còn mỗi quyển loại 120 trang được giảm 10%. Nếu năm học trước bạn Nam đạt danh hiệu học sinh giỏi thì bạn chỉ phải trả bao nhiêu tiền cho số vở trên.
Số tiền Nam được giảm khi mua 4 quyển vở loại 200 trang, 22 quyển vở loại 120 trang là:
\(13500. 4. 5\% {\rm{ }} + {\rm{ }}9500. 22. 10\% = 23600\) đồng.
Số tiền bạn phải trả nếu được giảm giá là:
\(263000--23600 = 239400\) (đồng).

