Câu hỏi:
2 năm trước
Hình thang \(ABCD\) có đáy \(CD\) gấp đôi đáy \(AB\) và diện tích tam giác \(ACD\) là \(30\,c{m^2}\). Diện tích của hình thang \(ABCD\) là:
Trả lời bởi giáo viên
Đáp án đúng: c
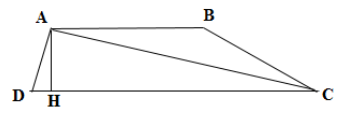
Kẻ đường cao \(AH\) của hình thang \(ABCD\).
Khi đó ta có: \({S_{ACD}} = \dfrac{1}{2}AH \times DC\) và \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right) \times AH}}{2}\).
Mà theo đề bài: \(CD = 2 \times AB\) nên ta có: \({S_{ACD}} = \dfrac{1}{2}AH \times 2AB\)\( = AH \times AB = 30c{m^2}\).
Suy ra: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right) \times AH}}{2}\)\( = \dfrac{{\left( {AB + 2AB} \right) \times AH}}{2} = \dfrac{{3AB \times AH}}{2}\)\( = \dfrac{{3 \times 30}}{2} = 45\,c{m^2}\).
Hướng dẫn giải:
Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.
Sử dụng công thức tính diện tích hình thang bằng nửa tích của tổng hai đáy với chiều cao.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
