Nước biển chứa 4% muối. Cần đổ thêm bao nhiêu gam nước lã vào \(400g\) nước biển để tỉ lệ muối trong dung dịch là 2%?
Lượng muối có trong \(400g\) nước biển là: \(4\% .400 = 16\) gam
Vì lượng muối không đổi nên lượng nước trong dung dịch \(2\% \) là: \(16:0,2 \times 100 = 800\) gam
Lượng nước cần thêm vào là: \(800 - 400 = 400\) gam
Từ trái nghĩa với nóng là:

a. lạnh
a. lạnh
a. lạnh
Từ có nghĩa trái ngược với nóng là: lạnh
Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)
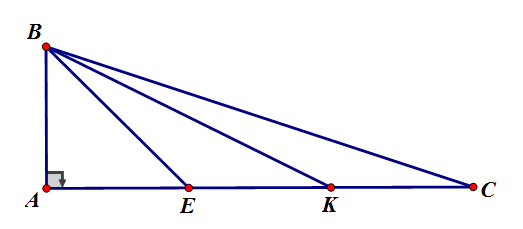
Tính \(BE\) và các tỉ số \(\dfrac{{BE}}{{EK}};\) \(\dfrac{{CE}}{{EB}}\).
Vì \(AE = 2cm;AC = 6cm \Rightarrow EC = 4cm\)
Lại có \(K\) là trung điểm \(EC\) nên \(EK = KC = \dfrac{{EC}}{2} = 2cm\)
Ta có: \(AE = EK = KC = {\rm{ }}2cm\)
Xét tam giác \(ABE\) vuông tại \(A.\) Theo định lý Pytago ta có \(B{E^2} = A{B^2} + A{E^2}\)\( = {2^2} + {2^2} = 8\).
Suy ra: \(BE = 2\sqrt 2 \,cm\).
Từ đó suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \) và \(\dfrac{{CE}}{{EB}} = \dfrac{4}{{2\sqrt 2 }} = \sqrt 2 \).
Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)

Chọn câu đúng.
Từ câu trước ta có: \(\dfrac{{BE}}{{EK}} = \sqrt 2 ;\dfrac{{CE}}{{EB}} = \sqrt 2 \) suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
Xét tam giác \(\Delta BEK\)và \(\Delta CEB\) có:
+) \(\dfrac{{BE}}{{EK}} = \dfrac{{CE}}{{EB}}\)
+) \(\widehat {CEB}\) chung
Suy ra: \(\Delta BEK \backsim \Delta CEB\) (c – g - c)
Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)

Tính \(\widehat {BKE} + \widehat {BCE}\).
Tam giác \(EBA\) vuông cân tại \(A\) nên \(\widehat {BEA} = {45^0}.\)
Từ câu trước ta có: \(\Delta BEK \backsim \Delta CEB\)
Suy ra: \(\widehat {BKE} = \widehat {CBE}\)
Do đó: \(\widehat {BKE} + \widehat {BCE} = \widehat {CBE} + \widehat {BCE}\)
Ta lại có: \(\widehat {BEA}\)là góc ngoài của tam giác \(EBC\) nên \(\widehat {CBE} + \widehat {BCE} = \widehat {BEA} = {45^0}\)
Nên \(\widehat {BKE} + \widehat {BCE} = {45^0}.\)
Con hãy tìm lỗi sai trong câu sau :

Các
vận
động
viên
đã
vào
đường
chạy
để
xẵn xàng
cho
cuộc
đua.
Các
vận
động
viên
đã
vào
đường
chạy
để
xẵn xàng
cho
cuộc
đua.
+ Từ viết sai : xẵn xàng
+ Viết đúng : sẵn sàng
Cho các số thực dương \(x,{\rm{ }}y,{\rm{ }}z\) thỏa mãn: \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\). Tìm giá trị lớn nhất của biểu thức \(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\).
Bổ đề: Với x,y dương là hai số bất kỳ thì: \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\).
Chứng minh: Vì x, y dương nên \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow {(x + y)^2} \ge 4xy\)
\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) với mọi x, y thỏa mãn yêu cầu.
Áp dụng bổ đề trên ta có: \(\dfrac{4}{{2x + y + z}} = \dfrac{4}{{\left( {x + y} \right) + \left( {x + z} \right)}} \le \dfrac{1}{{x + y}} + \dfrac{1}{{x + z}}\).
Cũng có: \(\dfrac{1}{{x + y}} + \dfrac{1}{{x + z}} \le \dfrac{1}{4}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{x} + \dfrac{1}{z}} \right) = \dfrac{1}{4}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\).
Do đó: \(\dfrac{1}{{2x + y + z}} \le \dfrac{1}{{16}}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\).
Tương tự ta có:
\(\dfrac{1}{{x + 2y + z}} \le \dfrac{1}{{16}}\left( {\dfrac{1}{x} + \dfrac{2}{y} + \dfrac{1}{z}} \right)\)
\(\)
\(\dfrac{1}{{x + y + 2z}} \le \dfrac{1}{{16}}\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{2}{z}} \right)\).
Cộng vế với vế các bất đẳng thức trên kết hợp với điều kiện \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\) ta có:
\(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\)\( \le \dfrac{1}{{16}}\left( {\dfrac{2}{x} + \dfrac{1}{y} + \dfrac{1}{z} + \dfrac{1}{x} + \dfrac{2}{y} + \dfrac{1}{z} + \dfrac{1}{x} + \dfrac{1}{y} + \dfrac{2}{z}} \right)\)
\(P \le \dfrac{1}{{16}}\left( {\dfrac{4}{x} + \dfrac{4}{y} + \dfrac{4}{z}} \right) = \dfrac{1}{{16}}.4\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)\)\( = \dfrac{1}{4}.4 = 1\).
Hay \(\dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}} \le 1\).
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x + y = x + z\\x + y = y + z\\x + z = y + z\\\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} = 4\end{array} \right.\)\( \Leftrightarrow x = y = z = \dfrac{3}{4}\).
Vậy giá trị lớn nhất của \(P = \dfrac{1}{{2x + y + z}} + \dfrac{1}{{2y + x + z}} + \dfrac{1}{{2z + x + y}}\) là \(1.\)
Giá trị của tổng \(\dfrac{1}{{5.10}} + \dfrac{1}{{10.15}} + \dfrac{1}{{15.20}} + ... + \dfrac{1}{{90.95}} + \dfrac{1}{{95.100}}\) là:
Xét: \(B = \dfrac{1}{{5.10}} + \dfrac{1}{{10.15}} + \dfrac{1}{{15.20}} + ... + \dfrac{1}{{90.95}} + \dfrac{1}{{95.100}}\)
Thì \(5B = \dfrac{5}{{5.10}} + \dfrac{5}{{10.15}} + \dfrac{5}{{15.20}} + ... + \dfrac{5}{{90.95}} + \dfrac{5}{{95.100}}\)
Ta có: \(\dfrac{5}{{5.10}} = \dfrac{1}{5} - \dfrac{1}{{10}}\)
\(\dfrac{5}{{10.15}} = \dfrac{1}{{10}} - \dfrac{1}{{15}}\)
\(\dfrac{5}{{15.20}} = \dfrac{1}{{15}} - \dfrac{1}{{20}}\)
…
\(\dfrac{5}{{90.95}} = \dfrac{1}{{90}} - \dfrac{1}{{95}}\)
\(\dfrac{5}{{95.100}} = \dfrac{1}{{95}} - \dfrac{1}{{100}}\)
Suy ra: \(5B = \dfrac{5}{{5.10}} + \dfrac{5}{{10.15}} + \dfrac{5}{{15.20}} + ... + \dfrac{5}{{90.95}} + \dfrac{5}{{95.100}}\)
\( = \dfrac{1}{5} - \dfrac{1}{{10}} + \dfrac{1}{{10}} - \dfrac{1}{{15}} + .... + \dfrac{1}{{90}} - \dfrac{1}{{95}} + \dfrac{1}{{95}} - \dfrac{1}{{100}}\)
\(\begin{array}{l} = \dfrac{1}{5} - \dfrac{1}{{100}}\\ = \dfrac{{19}}{{100}}\end{array}\)
Do đó: \(B = \dfrac{{19}}{{100}}:5 = \dfrac{{19}}{{500}}\)
Tìm \(x\) biết: \(\left( {6,27 - 1,38} \right):\left( {x{\rm{ : 2}}} \right) = 3,26\)
\(\left( {6,27 - 1,38} \right):\left( {x{\rm{ : 2}}} \right) = 3,26\)
\(\begin{array}{l}4,89:\left( {x:2} \right) = 3,26\\x:2 = 4,89:3,26\\x:2 = 1,5\\x = 1,5{\rm{ \times 2}}\\{\rm{x = 3}}\end{array}\)
Một miếng đất hình chữ nhật chu vi bằng \(152m,\) biết rằng nếu giảm chiều dài miếng đất 5m thì diện tích miếng đất giảm \(170{m^2}.\) Tính diện tích miếng đất.
Nửa chu vi hình chữ nhật ban đầu là: \(152:2 = 76{\rm{ }}m\)
Chiều rộng hình chữ nhật lúc đầu là: \(170:5 = 34{\rm{ }}m\)
Chiều dài hình chữ nhật lúc đầu là: \(76{\rm{ }}-34 = 42{\rm{ }}m\)
Diện tích miếng đất hình chữ nhật lúc đầu là: \(34 \times 42 = 1428\,{m^2}\)
Tìm một số tự nhiên A có 2 chữ số, biết rằng nếu viết chữ số 0 xen giữa chữ số hàng chục và hàng đơn vị của số A ta được số B lớn gấp 10 lần số A, nếu viết thêm chữ số 1 vào bên trái số B thì ta được số C lớn gấp 3 lần số B.
Gọi số A là \(\overline {ab} \).
Vì nếu viết chữ số 0 xen giữa chữ số hàng chục và hàng đơn vị của số A ta được số B lớn gấp 10 lần số A nên \(\overline {a0b} = 10{\rm{ }} \times {\rm{ }}\overline {{\rm{ab}}} \)
Do đó b = 0. Ta được \(B = \overline {a00} \)
Nếu viết thêm chữ số 1 vào bên trái số B thì ta được số C lớn gấp 3 lần số B.
Nên \(\overline {{\rm{1a00}}} = 3{\rm{ }} \times {\rm{ }}\overline {{\rm{a00}}} \)
\(\begin{array}{l}{\rm{1000 + }}\overline {{\rm{a00}}} {\rm{ = 3 }} \times {\rm{ }}\overline {{\rm{a00}}} {\rm{ }}\\{\rm{2 }} \times {\rm{ }}\overline {{\rm{a00}}} {\rm{ = 1000 }}\\\overline {{\rm{a00}}} {\rm{ = 500}}\\a \times 100 = 500\\{\rm{a = 5}}\end{array}\)
Vậy \(A = 50\)
Một của hàng rau quả có 2 rổ đựng cam và bưởi. Sau khi bán hết \(\dfrac{2}{5}\)số cam và \(\dfrac{4}{9}\) số bưởi, người bán hàng thấy rằng cả hai loại còn lại 165 quả, trong đó: số bưởi bằng \(\dfrac{2}{9}\) số cam. Hỏi lúc đầu cửa hàng đó có bao nhiêu quả mỗi loại?
Phân số chỉ số cam còn lại là: \(1 - \dfrac{2}{5} = \dfrac{3}{5}\) (số cam)
Phân số chỉ số bưởi còn lại là: \(1 - \dfrac{4}{9} = \dfrac{5}{9}\) (số bưởi).
Tổng số cam và số bưởi còn lại là: \(165\) quả và số bưởi bằng \(\dfrac{2}{9}\) số cam.
Coi số cam \(9\) phần thì số bưởi chiếm \(2\) phần. Tổng số phần bằng nhau là: \(9 + 2 = 11\) phần.
Số cam còn lại là: \(165:\left( {2 + 9} \right) \times 9 = 135\) (quả)
Số bưởi còn lại là: \(165-135 = 30\) (quả)
Số cam lúc đầu là: \(135:\dfrac{3}{5} = 225\) (quả)
Số bưởi lúc đầu là: \(30:\dfrac{5}{9} = 54\) (quả)

