Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)
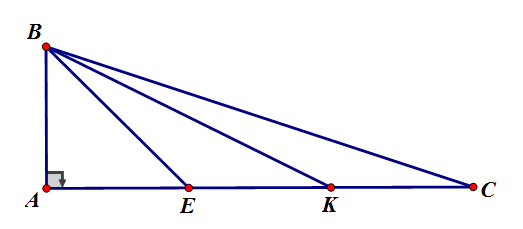
Tính \(\widehat {BKE} + \widehat {BCE}\).
Trả lời bởi giáo viên
Tam giác \(EBA\) vuông cân tại \(A\) nên \(\widehat {BEA} = {45^0}.\)
Từ câu trước ta có: \(\Delta BEK \backsim \Delta CEB\)
Suy ra: \(\widehat {BKE} = \widehat {CBE}\)
Do đó: \(\widehat {BKE} + \widehat {BCE} = \widehat {CBE} + \widehat {BCE}\)
Ta lại có: \(\widehat {BEA}\)là góc ngoài của tam giác \(EBC\) nên \(\widehat {CBE} + \widehat {BCE} = \widehat {BEA} = {45^0}\)
Nên \(\widehat {BKE} + \widehat {BCE} = {45^0}.\)
Hướng dẫn giải:
Sử dụng kết quả câu trước \(\Delta BEK \backsim \Delta CEB\).
Sử dụng: Góc ngoài của tam giác tại một đỉnh bằng tổng hai góc trong không kề với đỉnh đó.

