Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) có \(\widehat A\, = \,{90^0}\), \(AB = 2cm,AC = 6cm.\) Trên cạnh \(AC\) lấy điểm \(E,{\rm{ }}K\) sao cho \(AE = 2cm\) và \(K\) là trung điểm của đoạn thẳng \(EC.\)
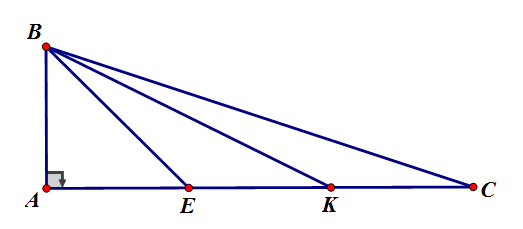
Tính \(BE\) và các tỉ số \(\dfrac{{BE}}{{EK}};\) \(\dfrac{{CE}}{{EB}}\).
Trả lời bởi giáo viên
Đáp án đúng: c
Vì \(AE = 2cm;AC = 6cm \Rightarrow EC = 4cm\)
Lại có \(K\) là trung điểm \(EC\) nên \(EK = KC = \dfrac{{EC}}{2} = 2cm\)
Ta có: \(AE = EK = KC = {\rm{ }}2cm\)
Xét tam giác \(ABE\) vuông tại \(A.\) Theo định lý Pytago ta có \(B{E^2} = A{B^2} + A{E^2}\)\( = {2^2} + {2^2} = 8\).
Suy ra: \(BE = 2\sqrt 2 \,cm\).
Từ đó suy ra: \(\dfrac{{BE}}{{EK}} = \dfrac{{2\sqrt 2 }}{2} = \sqrt 2 \) và \(\dfrac{{CE}}{{EB}} = \dfrac{4}{{2\sqrt 2 }} = \sqrt 2 \).
Hướng dẫn giải:
Áp dụng định lí Pitago để tính độ dài cạnh \(BE\). Từ đó tính các tỉ số.
Câu hỏi khác
- Đề thi khảo sát chất lượng đầu năm - Đề số 1 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 2 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 4 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 5 toán 9 có lời giải
- Đề thi khảo sát chất lượng đầu năm - Đề số 3 toán 9 có lời giải
