Tính diện tích tam giác \(DMN,\) nếu biết diện tích tam giác \(ABC\) là: \(640\,c{m^2}.\)

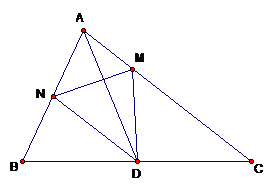
Nhận thấy hai tam giác \(ANC\) và \(ABC\) có chung chiều cao hạ từ đỉnh \(C\)

Mà \(AN = \dfrac{1}{2} \times AB\) nên \({S_{{\rm{ANC}}}} = \dfrac{1}{2}{S_{ABC}}{\rm{ }}\)

Nhận thấy hai tam giác \(ANM\) và \(ANC\) có chung chiều cao hạ từ đỉnh \(N\) mà \(AM = \dfrac{1}{3} \times AC\) nên \({{\rm{S}}_{{\rm{AMN}}}} = \dfrac{1}{3} \times {\rm{ }}{{\rm{S}}_{{\rm{ANC}}}}\).

Do đó: \({S_{AMN}} = \dfrac{1}{3} \times {S_{ANC}}\)\( = \dfrac{1}{3} \times \dfrac{1}{2} \times {S_{ABC}} = \dfrac{1}{6} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}}\)

Vậy \({S_{AMN}} = \dfrac{1}{6} \times {S_{ABC}}\)

Tương tự ta có: \({{\rm{S}}_{{\rm{DMC}}}} = \dfrac{1}{3} \times {{\rm{S}}_{{\rm{ABC}}}}{\rm{ ;\,}}{{\rm{S}}_{{\rm{DNB}}}} = \dfrac{1}{4} \times {{\rm{S}}_{{\rm{ABC}}}}\)

Mà \({S_{DMN}} + {S_{AMN}} + {S_{BDN}} + {S_{DCM}} = {S_{ABC}}\)

Nên  \({S_{DMN}} = {S_{ABC}} - {S_{AMN}} - {S_{BDN}} - {S_{DCM}}\)\( = {S_{ABC}} - \dfrac{1}{6} \times {S_{ABC}} - \dfrac{1}{4} \times {S_{ABC}} - \dfrac{1}{3} \times {S_{ABC}} = \dfrac{1}{4} \times {S_{ABC}}\)

Do đó: \({S_{DMN}} = \dfrac{1}{4} \times {\rm{ }}{{\rm{S}}_{{\rm{ABC}}}} = \dfrac{1}{4} \times {\rm{ 640 = 160c}}{{\rm{m}}^{\rm{2}}}\)