Đề thi khảo sát chất lượng đầu năm - Đề số 1

Diện tích toàn phần của hình lập phương có độ dài cạnh đáy bằng 5cm là: \({S_{tp}} = {6. 5^2} = 150\,c{m^2}.\)

Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK.

Theo bài ta có:

\(\Delta MNP \backsim \Delta HGK\) và \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}\)

\( \Rightarrow \dfrac{{MN}}{{HG}} = \dfrac{{NP}}{{GK}} = \dfrac{{MP}}{{HK}} \)\(=\dfrac{MN+NP+MP}{HG+GK+HK}= \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} = k\)

Do đó: \(  \dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)

Và \( \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = {k^2} = {\left( {\dfrac{2}{7}} \right)^2} = \dfrac{4}{{49}}.\)

Đáp án đúng là: 

Những đóa hoa đang nở để đón mùa xuân. Còn bướm ong đang bay rập rờn. Nắng vàng làm những hạt sương lóng lánh.

\(10\% \) của \(8dm\) là \(10 \times 8:100 = 80:100 = 0,8dm = 8cm\).

Ta có:

+) Đáp án A: \(2x + 5 > 11 \Leftrightarrow 2x > 6 \)\(\Leftrightarrow x > 3 \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.

+) Đáp án B: \(4 - x > 3x - 1 \Leftrightarrow 4 + 1 > 3x + x \Leftrightarrow 4x < 5\)\( \Leftrightarrow x < \dfrac{5}{4} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.

+) Đáp án C: \( - 4x + 7 > x - 1 \Leftrightarrow 7 + 1 > x + 4x \Leftrightarrow 5x < 8\)\( \Leftrightarrow x < \dfrac{8}{5} \Rightarrow x = 2\) không thuộc tập nghiệm của bất phương trình.

+) Đáp án D: \({x^2} + 3 > 6x - 7 \Leftrightarrow {x^2} - 6x + 10 > 0\)

Thay \(x = 2\) vào vế trái của bất phương trình ta có: \({2^2} - 6.2 + 10 = 2 > 0\) (luôn đúng)

\( \Rightarrow x = 2\) là nghiệm của bất phương trình.

Đáp án đúng là:

Nắng vàng làm những hạt sương lóng lánh. Thế mà bé cứ tưởng là bong bóng. Bé sờ vào, nó vỡ ra tạo thành một dòng nước cuốn bé trôi xuống đất.

Ta có: \({\left( {x + y} \right)^2} + {\rm{ }}{\left( {x - y} \right)^2}\)\( = {x^2} + 2xy + {y^2} + {x^2} - 2xy + {y^2}\)\( = 2{x^2} + 2{y^2} = 2\left( {{x^2} + {y^2}} \right)\).

Ta có: \(3\dfrac{5}{4} = \dfrac{{3 \times 4 + 5}}{4} = \dfrac{{12 + 5}}{4} = \dfrac{{17}}{4}\).

Ta có: \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\)\( = 5{x^2}{y^3}. 1 - 5{x^2}{y^3}. 5xy + 5{x^2}{y^3}. 2x\)\( = 5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\).

Các số tự nhiên nhỏ hơn \(4\) là \(0,1,2,3\).

Tập hợp \(B = \left\{ {0;1;2;3} \right\}\).

Ta có: \(7x + 4\; = 3x-{\rm{ }}1\)

\(\begin{array}{l} \Leftrightarrow 7x - 3x = - 1 - 4\\ \Leftrightarrow 4x = - 5\\ \Leftrightarrow x = - \dfrac{5}{4}\end{array}\).

Vậy phương trình có tập nghiệm là \(S = \left\{ {\dfrac{{ - 5}}{4}} \right\}\).

Ta có: \({x^3} - 9x = 0\)\( \Leftrightarrow x\left( {{x^2} - 9} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 9 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\\x = - 3\end{array} \right.\)

Vậy phương trình có tập nghiệm \(S = \left\{ { - 3;0;3} \right\}\).

Hay phương trình đã cho có ba nghiệm phân biệt.

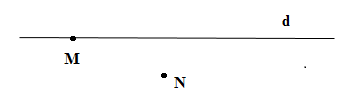
Từ hình vẽ ta tháy điểm \(M\) nằm trên đường thẳng \(d\) và điểm \(N\) không nằm trên đường thẳng \(d\) nên \(M \in d;N \notin d.\)

Xét phương trình \(\left| {x - 4} \right| + 3x = 5\).

TH1: \(\left| {x - 4} \right| = x - 4\) với \(x - 4 \ge 0 \Leftrightarrow x \ge 4\)

Khi đó ta có phương trình: \(x - 4 + 3x = 5 \Leftrightarrow 4x = 9 \Leftrightarrow x = \dfrac{9}{4}\) (loại)

TH2: \(\left| {x - 4} \right| =  - x + 4\) với \(x - 4 < 0 \Leftrightarrow x < 4\)

Khi đó ta có phương trình \( - x + 4 + 3x = 5\)\( \Leftrightarrow 2x = 1 \Leftrightarrow x = \dfrac{1}{2}\) (nhận)

Vậy phương trình đã cho có một nghiệm là \(x = \dfrac{1}{2}.\)

Bài văn trên nói về ông của tác giả.

=> Đáp án: b

Ta có: \(\dfrac{3}{2}.\dfrac{4}{5}:x = \dfrac{2}{3}\).

\(\begin{array}{l}\dfrac{6}{5}:x = \dfrac{2}{3}\\x = \dfrac{6}{5}:\dfrac{2}{3}\\x = \dfrac{6}{5}.\dfrac{3}{2}\\x = \dfrac{9}{5}\end{array}\).

ĐKXĐ: \(x \ne  \pm 5\)

Ta có: \(\dfrac{{x + 5}}{{x - 5}} - \dfrac{{x - 5}}{{x + 5}} = \dfrac{{20}}{{{x^2} - 25}}\).

\( \Leftrightarrow \dfrac{{{{\left( {x + 5} \right)}^2} - {{\left( {x - 5} \right)}^2}}}{{\left( {x + 5} \right)\left( {x - 5} \right)}} = \dfrac{{20}}{{\left( {x + 5} \right)\left( {x - 5} \right)}}\)

\(\begin{array}{l} \Rightarrow {\left( {x + 5} \right)^2} - {\left( {x - 5} \right)^2} = 20\\ \Leftrightarrow {x^2} + 10x + 25 - {x^2} + 10x - 25 = 20\\ \Leftrightarrow 20x = 20\\ \Leftrightarrow x = 1\left( {tm} \right)\end{array}\)

Vậy phương trình đã cho có tập nghiệm \(S = \left\{ 1 \right\}\).

Ông của tác giả làm nghề thợ hàn.

=> Đáp án: a

Ta có: \(95m = \dfrac{{95}}{{1000}} = 0,095km\).

\(Q = \left( {\dfrac{{{x^2} - 1}}{{x - 1}} + \dfrac{{{x^3} - 1}}{{1 - {x^2}}}} \right):\dfrac{{2{x^2} - 4x + 2}}{{{x^2} - 1}}\quad \left( {x \ne  \pm 1} \right)\)

\(Q = \left( {\dfrac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}} - \dfrac{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} \right):\dfrac{{2{{\left( {x - 1} \right)}^2}}}{{{x^2} - 1}}\)

\(Q = \left( {\dfrac{{x + 1}}{1} - \dfrac{{{x^2} + x + 1}}{{x + 1}}} \right):\dfrac{{2\left( {x - 1} \right)}}{{x + 1}}\)

\(Q = \dfrac{{{{\left( {x + 1} \right)}^2} - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\)

\(\begin{array}{l}Q = \dfrac{{{x^2} + 2x + 1 - {x^2} - x - 1}}{{x + 1}}.\dfrac{{x + 1}}{{2\left( {x - 1} \right)}}\\Q = \dfrac{x}{{2\left( {x - 1} \right)}}\end{array}\)

Vậy \(Q = \dfrac{x}{{2\left( {x - 1} \right)}}\) với mọi \(x \ne  \pm 1\).