Đề thi khảo sát chất lượng đầu năm - Đề số 1

Theo kết quả câu trước $Q = \dfrac{x}{{2\left( {x - 1} \right)}}$ với mọi $x \ne  \pm 1$.

Để $Q = 3$ thì $\dfrac{x}{{2\left( {x - 1} \right)}} = 3 \Rightarrow x = 3. 2\left( {x - 1} \right)$

$\Leftrightarrow x = 6x - 6 \Leftrightarrow 6x - x = 6 \Leftrightarrow 5x = 6$$\Leftrightarrow x = \dfrac{6}{5}\;\left( {tm} \right)$

Vậy $x = \dfrac{6}{5}$ thì $Q = 3.$

Ta có $\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q }} \Leftrightarrow {\rm{ Q  <  0}}$

Khi đó ta được:  $\dfrac{x}{{2\left( {x - 1} \right)}}$ < 0   $\forall x \ne  \pm 1$

TH1: $\left\{ \begin{array}{l}x < 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x < 0\\x > 1\end{array} \right.$    không xảy ra.

TH2: $\left\{ \begin{array}{l}x > 0\\x - 1 < 0\end{array} \right. \Leftrightarrow {\rm{ 0  <  x  <  1}}$.

Vậy với ${\rm{ 0  <  x  <  1}}$ thì $\left| {\rm{Q}} \right|{\rm{ }} > {\rm{ Q}}$.

Với gia đình, ông là niềm tự hào.

=> Đáp án: b

Diện tích tam giác là $\dfrac {1}{2}\times 6,6 \times 2,4 = 7,92\,c{m^2}$.

Đổi 10 phút = $\dfrac{1}{6}$ giờ.

Gọi quãng đường AB dài là $x\left( {km} \right)\left( {x > 30{\rm{ }}} \right)$.

Suy ra quãng đường từ khi dừng lại sửa xe đến B là $x- 30{\rm{ }}\left( {km} \right)$.

Thời gian dự định đi từ A đến B là $\dfrac{x}{{30}}$(h).

Thời gian thực tế đi từ A đến B là $1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}}$ (h).

Ta có phương trình:

$1 + \dfrac{1}{6} + \dfrac{{x - 30}}{{36}} = \dfrac{x}{{30}}$

$\Leftrightarrow \dfrac{{36 + 6 + x - 30}}{{36}} = \dfrac{x}{{30}}$

$\begin{array}{l} \Leftrightarrow \dfrac{{12 + x}}{{36}} = \dfrac{x}{{30}}\\ \Rightarrow 30\left( {12 + x} \right) = 36.x\\ \Leftrightarrow 360 + 30x = 36x\\ \Leftrightarrow 6x = 360\\ \Leftrightarrow x = 60\left( {tm} \right)\end{array}$

Vậy quãng đường $AB$ dài $60$ km.

Đáp án đúng là: 

   Ông tôi vốn là thợ gò hàn vào loại giỏi. Có lần, chính mắt tôi đã thấy ông tán đinh đồng. Chiếc búa trong tay ông hoa lên, nhát nghiêng, nhát thẳng,...

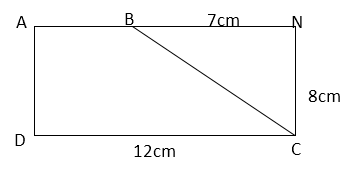
Độ dài cạnh $AB$ là $AB = AN - BN$$= DC - BN = 12 - 7 = 5cm$.

Độ dài cạnh $AB$ là $AB = NC = 8cm$.

Diện tích hình thang $ABCD$ bằng $S = \dfrac{{\left( {AB + CD} \right) \times AD}}{2}$$= \dfrac{{\left( {5 + 12} \right) \times 8}}{2} = 68\,c{m^2}.$

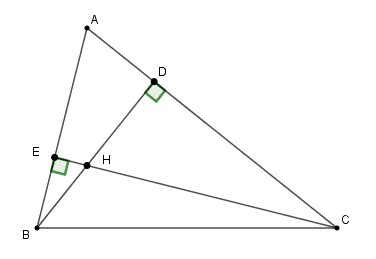
Xét $\Delta ABD$ và $\Delta ACE$ có:

$\widehat {\rm{A}}$ là góc chung, $\widehat {ADB} = \widehat {AEC} = {90^0}$

$\Rightarrow$ $\Delta ABD \backsim \Delta ACE$ (g-g)

$\Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}$$\Rightarrow AE.{\rm{ }}AB = AC. {\rm{ }}AD$.

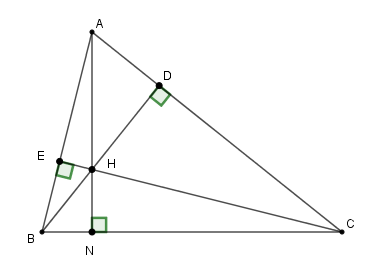
Kẻ $AH$ cắt $BC$ tại $N.$ Vì $H$ là giao điểm hai đường cao $BD,CE$ nên $H$ là trực tâm tam giác $ABC.$

Suy ra: $AH \bot BC$ hay $AN \bot BC.$

Xét $\Delta BHN$ và $\Delta BCD$ có: $\widehat B$ chung và $\widehat {HNB} = \widehat {BDC} = {90^0}$ nên $\Delta BHN \backsim \Delta BCD \left( {g - g} \right)$

Suy ra: $\dfrac{{BH}}{{BC}} = \dfrac{{BN}}{{BD}} \Rightarrow BH.BD = BN.BC$  (1)

Xét $\Delta CHN$ và $\Delta CBE$ có: $\widehat C$ chung và $\widehat {HNC} = \widehat {BEC} = {90^0}$ nên $\Delta CHN \backsim \Delta CBE \left( {g - g} \right)$

Suy ra: $\dfrac{{CH}}{{CB}} = \dfrac{{CN}}{{CE}} \Rightarrow CH.CE = CN.BC$ (2)

Từ (1) và (2) suy ra $BH.BD + CH.CE = BN.BC + CN.BC$$= BC\left( {CN + BN} \right) = BC.BC = B{C^2}$.

Vậy $BH.BD + CH.CE = B{C^2}.$

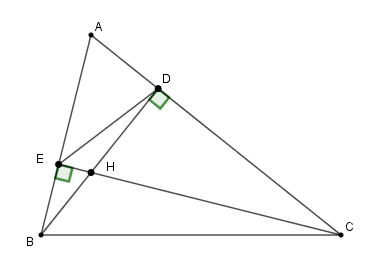
+) Xét $\Delta ABD$ và $\Delta ACE$ có:

$\widehat {\rm{A}}$ là góc chung, $\widehat {ADB} = \widehat {AEC} = {90^0}$

$\Rightarrow$ $\Delta ABD \backsim \Delta ACE$ (g-g)

$\Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}$

Xét $\Delta AED$ và $\Delta ACB$ có: $\widehat A$ chung và $\dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\left( {cmt} \right)$ nên $\Delta AED \backsim \Delta ACB\left( {c - g - c} \right)$

Từ đó: $\widehat {AED} = \widehat {ACB}$ (hai góc tương ứng)

Nên $\widehat {ACB} = {40^0}$. Lại có: $\Delta DBC$ vuông tại $D$ nên $\widehat {DCB} + \widehat {DBC} = {90^0}$$\Rightarrow \widehat {DBC} = {90^0} - {40^0} = {50^0}$

Hay $\widehat {HBC} = {50^0}$.

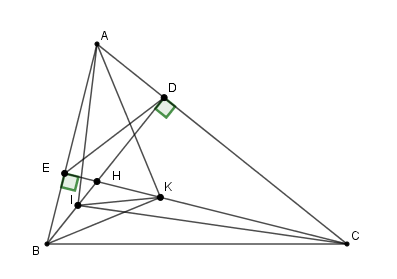
Xét $\Delta AID$ và $\Delta ACI$ có: $\widehat {IAD}$ chung và $\widehat {AIC} = \widehat {ADB} = {90^0}$ nên $\Delta AID \backsim \Delta ACI\left( {g - g} \right)$

Suy ra: $\dfrac{{AI}}{{AC}} = \dfrac{{AD}}{{AI}} \Leftrightarrow A{I^2} = AC.AD$  (1)

Xét $\Delta AEK$ và $\Delta AKB$ có: $\widehat {EAK}$ chung và $\widehat {AIC} = \widehat {ADB} = {90^0}$ nên $\Delta AEK \backsim \Delta AKB\left( {g - g} \right)$

Suy ra: $\dfrac{{AE}}{{AK}} = \dfrac{{AK}}{{AB}} \Leftrightarrow A{K^2} = AE.AB$ (2)

Xét $\Delta ABD$ và $\Delta ACE$ có:

$\widehat {\rm{A}}$ là góc chung, $\widehat {ADB} = \widehat {AEC} = {90^0}$

$\Rightarrow$ $\Delta ABD \backsim \Delta ACE\left( {g - g} \right)$

$\Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}$ $\Rightarrow AE.{\rm{ }}AB = AC.{\rm{ }}AD$ (3)

Từ (1), (2) và (3) suy ra: $A{I^2} = A{K^2} \Rightarrow AI = AK$ nên tam giác $AIK$ cân tại $A.$

Đáp án đúng là:

   Có lần, chính mắt tôi đã thấy ông tán đinh đồng. Chiếc búa trong tay ông hoa lên, nhát nghiêng, nhát thẳng, nhanh đến mức tôi chỉ cảm thấy trước mặt ông phất phơ những sợi tơ mỏng.

Ta có:

$\begin{array}{l}8,16:\left( {1,32 + 3,48} \right) - 0,45:2\\ = \;\;8,16:\;4,8 - \;0,45:2\\ = 1,7 - \;\;0,225\\\; = 1,475\;\end{array}$.

Đặt $x = 1 + 6a; y = 1 + 2b; z = 1 + 3c\,\,\left( {x,y,z > 0} \right)$

$\Rightarrow x + y + z = 1 + 6a + 1 + 2b + 1 + 3c$$= 3 + \left( {6a + 2b + 3c} \right) = 3 + 11 = 14$

Ta có: $2b + 3c + 16 = y - 1 + z - 1 + 16 = y + z + 14$

$6a + 3c + 16 = x + z + 14$

$6a + 2b + 16 = x + y + 14$

Từ đó: $M = \dfrac{{z + y + 14}}{x} + \dfrac{{x + z + 14}}{y} + \dfrac{{x + y + 14}}{z}$

$= \dfrac{z}{x} + \dfrac{y}{x} + \dfrac{{14}}{x} + \dfrac{x}{y} + \dfrac{z}{y} + \dfrac{{14}}{y} + \dfrac{x}{z} + \dfrac{y}{z} + \dfrac{{14}}{z}$

$= \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 14\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)$

$= \left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + \left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + \left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + \left( {x + y + z} \right)\left( {\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z}} \right)$

$= 2\left( {\dfrac{x}{y} + \dfrac{y}{x}} \right) + 2\left( {\dfrac{y}{z} + \dfrac{z}{x}} \right) + 2\left( {\dfrac{z}{x} + \dfrac{x}{z}} \right) + 3$

Mặt khác: $\dfrac{x}{y} + \dfrac{y}{x} \ge 2$ dấu “ = ” xảy ra khi và chỉ khi $x = y$

$\dfrac{x}{z} + \dfrac{z}{x} \ge 2.$ Dấu “ = ” xảy ra khi và chỉ khi $x = z$

$\dfrac{z}{y} + \dfrac{y}{z} \ge 2.$ Dấu “ = ” xảy ra khi và chỉ khi $z = y$

Khi đó: $M \ge 2. 2 + 2. 2 + 2. 2 + 3 \Rightarrow M \ge 15.$ Dấu “ = ” xảy ra khi và chỉ khi $x = y = z = 1$

Suy ra: $a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.$

Vậy ${M_{min}} = 15$ khi $a = \dfrac{{11}}{{18}};b = \dfrac{{11}}{6};c = \dfrac{{11}}{9}.$

Đoạn văn trên có bốn dấu chấm.

=> Đáp án: b

Ta có:

$\begin{array}{l}\left( {x + 73} \right):5 = 20 + 7,5 \times 4\\\left( {x + 73} \right):5 = 20 + 30\\\left( {x + 73} \right):5 = 50\\x + 73 = 50 \times 5\\x + 73 = 250\\x = 250 - 73\\x = 177\end{array}$.

Vậy $x = 177.$

12% giá của chiếc cặp đó là:

$65000 \times 12:100 = 7800$ (đồng)

Sau khi giảm giá $12\% ,$ giá của chiếc cặp là:

$65000 - 7800 = 57200$ (đồng)

Đáp số: $57200$ đồng.

Chiều cao của phòng học là: $6 \times \dfrac{2}{3} = 4\,\left( m \right)$.

Thể tích của phòng học đó là: $8 \times 6 \times 4 = 192\left( {{m^3}} \right)$.

Phòng học đó chứa được số mét khối không khí là: $192 - 3 = 189\left( {{m^3}} \right)$.

Đáp số: $189{\rm{ }}{m^3}$.

Nếu gấp cả hai số lên $3$ lần thì tổng của hai số lúc này là: $47,4 \times 3 = 142,2$.

Vì gấp số thứ nhất lên $3$ lần và số thứ hai lên $2$ lần thì tổng số là $129,4$.

Nên số thứ hai là: $142,2\; - 129,4 = 12,8$.

Số thứ nhất là: $47,4-12,8 = 34,6$.

Các đường thẳng tạo thành là $AB,AC,AD,BC,BD,CD.$

Vậy có $6$ đường thẳng tạo thành.