Câu hỏi:
3 năm trước
Cho \(\Delta ABC\) kẻ các đường cao \(BD\) và \(CE\) (\(D \in AC{\rm{ ; E}} \in {\rm{AB}}\)). \(BD\) và \(CE\) cắt nhau tại \(H.\)
Tích \(AE{\rm{ }}.{\rm{ }}AB\;\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
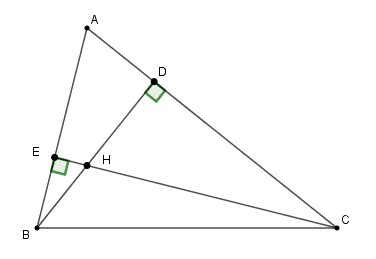
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(\widehat {\rm{A}}\) là góc chung, \(\widehat {ADB} = \widehat {AEC} = {90^0}\)
\( \Rightarrow \) \(\Delta ABD \backsim \Delta ACE\) (g-g)
\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{AB}}{{AC}}\)\( \Rightarrow AE.{\rm{ }}AB = AC. {\rm{ }}AD\).
Hướng dẫn giải:
Sử dụng trường hợp đồng dạng thứ ba góc - góc rồi suy ra hệ thức tương ứng về cạnh.

