Cho \(\Delta ABC\) kẻ các đường cao \(BD\) và \(CE\) (\(D \in AC{\rm{ ; E}} \in {\rm{AB}}\)). \(BD\) và \(CE\) cắt nhau tại \(H.\)      

Hệ thức nào dưới đây đúng?

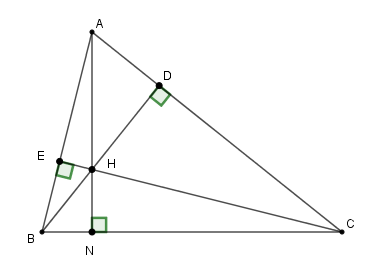
Kẻ \(AH\) cắt \(BC\) tại \(N.\) Vì \(H\) là giao điểm hai đường cao \(BD,CE\) nên \(H\) là trực tâm tam giác \(ABC.\)

Suy ra: \(AH \bot BC\) hay \(AN \bot BC.\)

Xét \(\Delta BHN\) và \(\Delta BCD\) có: \(\widehat B\) chung và \(\widehat {HNB} = \widehat {BDC} = {90^0}\) nên \(\Delta BHN \backsim \Delta BCD \left( {g - g} \right)\)

Suy ra: \(\dfrac{{BH}}{{BC}} = \dfrac{{BN}}{{BD}} \Rightarrow BH.BD = BN.BC\)  (1)

Xét \(\Delta CHN\) và \(\Delta CBE\) có: \(\widehat C\) chung và \(\widehat {HNC} = \widehat {BEC} = {90^0}\) nên \(\Delta CHN \backsim \Delta CBE \left( {g - g} \right)\)

Suy ra: \(\dfrac{{CH}}{{CB}} = \dfrac{{CN}}{{CE}} \Rightarrow CH.CE = CN.BC\) (2)

Từ (1) và (2) suy ra \(BH.BD + CH.CE = BN.BC + CN.BC\)\( = BC\left( {CN + BN} \right) = BC.BC = B{C^2}\).

Vậy \(BH.BD + CH.CE = B{C^2}.\)