Câu hỏi:
3 năm trước
Cho tam giác ABC vuông tại A (\(AB < AC\)) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Chọn khẳng định đúng:
Trả lời bởi giáo viên
Đáp án đúng: d
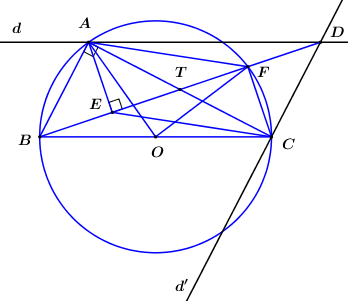
Do tứ giác \(AECD\) nội tiếp (cmt) nên: \(\angle CAE = \angle CDE\) (hai góc nội tiếp cùng chắn cung \(CE\))
Mà \(\angle CDE = \angle ABF\) (so le trong)
\( \Rightarrow \angle CAE = \angle ABF\).
Mặt khác: \(\angle AOF = 2\angle ABF\) (góc ở tâm và góc nội tiếp cùng chắn cung \(AF\))
\( \Rightarrow \angle AOF = 2\angle CAE\).
Hướng dẫn giải:
Vận dụng tính của góc trong tứ giác nội tiếp và góc ở tâm và góc nội tiếp cùng chắn một cung.

