Câu hỏi:
2 năm trước
Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)
Tứ giác \(AIDG\) nội tiếp đường tròn nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
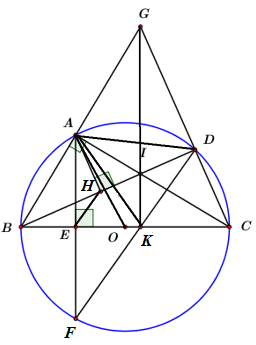
Ta có: \(\angle BAC,\)\(\angle BDC\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)\( \Rightarrow \angle BAC = \angle BDC = {90^0}.\)
\( \Rightarrow \angle GAI = \angle GDI = {90^0}\)
Xét tứ giác \(AIDG\) ta có: \(\angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}\)
Suy ra \(AIDG\) là tứ giác nội tiếp đường tròn đường kính \(GI\).
Hướng dẫn giải:
Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp: chứng minh \(\angle GAI + \angle GDI = {180^0}\)\(\angle ABC\) là tứ giác nội tiếp
