Cho \(\Delta ABC\,\,\,\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O\) đường kính \(BC\) cố định, điểm \(D\) bất kì thuộc cung nhỏ \(AC\)\(\left( {D \ne A,\,\,D \ne C} \right).\) Tia \(BA\) cắt tia \(CD\) tại điểm \(G.\) Điểm \(I\) là giao điểm của \(BD\) và \(AC.\) Kẻ \(AE\) vuông góc với \(BC\) tại điểm \(E,\) đường thẳng \(AE\) cắt đường tròn \(\left( O \right)\) tại điểm thứ hai là \(F.\) Gọi \(H\) là hình chiếu vuông góc của điểm \(A\) trên \(BD,\,\,K\) là giao điểm của \(BC\) và \(DF.\)

Đường tròn ngoại tiếp \(\Delta AKD\) luôn đi qua một điểm cố định khác \(A\) khi điểm \(D\) di động trên cung nhỏ \(AC\)?

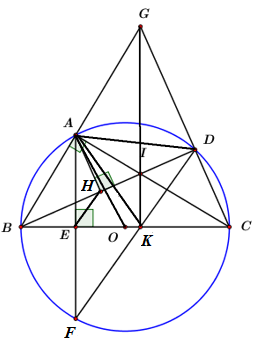
Ta có: \(OA = \dfrac{1}{2}BC = OB\) (đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \angle OAB = \angle OBA = \angle ABC = \dfrac{1}{2}\,\,sd\,\,cung\,\,AC\) \(\left( 3 \right)\)

Lại có: \(\angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cng\,\,BF} \right)\)\( = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + sd\,\,cung\,\,AB} \right)\)

Vì \(OH \bot BD\,\,\left( {gt} \right)\)\( \Rightarrow cung\,\,AB = cung\,\,AD\)

\( \Rightarrow \angle CKD = \dfrac{1}{2}\left( {sd\,\,cung\,\,CD + \,sd\,\,cung\,\,AD} \right)\)\( = \dfrac{1}{2}sd\,\,cung\,\,AC\,\,\,\left( 4 \right)\)

Từ \(\left( 3 \right)\) và \(\left( 4 \right)\) \( \Rightarrow \angle OAB = \angle CKD\)

\( \Rightarrow OKDA\) là tứ giác nội tiếp. (tứ giác có góc ngoài bằng góc trong tại đỉnh đối diện)

\( \Rightarrow \) Đường tròn ngoại tiếp \(\Delta AKD\) đi qua điểm \(O\) cố định.