Câu hỏi:
2 năm trước
Cho tam giác ABC vuông tại A (\(AB < AC\)) nội tiếp trong đường tròn tâm O. Dựng đường thẳng d đi qua A song song với BC, đường thẳng d’ qua C song song BA, gọi D là giao điểm của d và d’. Dựng AE vuông góc với BD (E nằm trên BD), F là giao điểm của BD với đường tròn (O).
Tứ giác \(AECD\) nội tiếp đường tròn nào dưới đây:
Trả lời bởi giáo viên
Đáp án đúng: c
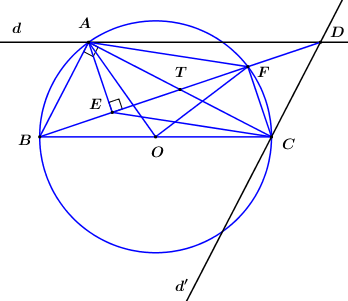
Vì \(\Delta ABC\) vuông tại \(A\) và nội tiếp \(\left( O \right)\) nên \(BC\) là đường kính của \(\left( O \right)\).
Ta có: \(\left\{ \begin{array}{l}AB \bot AC\\CD//AB\end{array} \right.\,\,\left( {gt} \right) \Rightarrow AC \bot CD\) (từ vuông góc đến song song) \( \Rightarrow \angle ACD = {90^0}\).
Xét tứ giác \(AECD\) có: \(\angle AED = \angle ACD = {90^0}\) \( \Rightarrow AECD\) là tứ giác nội tiếp đường tròn đường kính AD. (Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau).
Hướng dẫn giải:
Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: Tứ giác có 2 đỉnh kề cùng nhìn một cạnh dưới các góc bằng nhau là tứ giác nội tiếp.
