Cho tam giác \(ABC\) cân tại \(A,\) nội tiếp đường tròn \(\left( {O;R} \right).\) Gọi \(D\) là trung điểm của \(AC;\) tia \(BD\) cắt tiếp tuyến tại \(A\) với đường tròn \(\left( O \right)\) tại điểm \(E;\,EC\) cắt \(\left( O \right)\) tại \(F.\) Giả sử rằng \(DF//BC.\) Khi đó \(cos\,\widehat {ABC} = ?\)

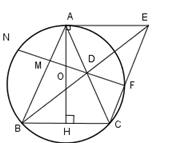
Giả sử rằng tia \(FD\) cắt \(AB\) tại \(M,\) cắt \(\left( O \right)\) tại \(N.\) Theo giả thiết \(DF//BC,\) và \(AH\) là trục đối xứng của \(BC\) và của đường tròn \(\left( O \right)\) nên \(F,\,D\) theo thứ tự là điểm đối xứng với \(N,\,M\) qua \(AH.\)

Do đó \(FD = MN = MD = \dfrac{1}{2}BC = \dfrac{1}{2}ND = BH\,\,\left( 1 \right).\)

Xét \(\Delta NDA,\,\Delta CDF\) có \(\widehat {ADN} = \widehat {CDF}\) (hai góc đối đỉnh).

\(\widehat {ACF},\,\widehat {FNA}\) là hai góc nội tiếp chắn cung \(AF\) nên \(\widehat {DCF} = \widehat {DNA}\)

Do đó \(\Delta NDA \backsim \Delta CDF\)\( \Rightarrow \dfrac{{DA}}{{DF}} = \dfrac{{ND}}{{CD}} \Rightarrow DF.DN = DA.DC\,\,\left( 4 \right).\)

Từ (1), (4) suy ra \(2B{H^2} = \dfrac{1}{4}A{C^2}\) \( \Rightarrow BH = \dfrac{{\sqrt 2 }}{4}AC \Rightarrow \cos \,\widehat {ABC} = \dfrac{{BH}}{{AB}} = \dfrac{{BH}}{{AC}} = \dfrac{{\sqrt 2 }}{4}.\)