Cho đường tròn \(\left( {O;R} \right)\)và một điểm \(M\) bên trong đường tròn đó. Qua \(M\) kẻ hai dây cung \(AB\) và \(CD\) vuông góc với nhau (\(C\) thuộc cung nhỏ \(AB\)). Vẽ đường kính \(DE.\) Cho biết thêm rằng \(R = 1.\) Giá trị lớn nhất của biểu thức \(Q = MA + MB + MC + MD\) là:

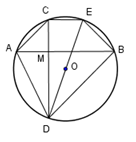
Do \(DE\) là đường kính của \(\left( {O;R} \right)\) nên \(\widehat {DCE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).

Do đó \(CD \bot CE.\) Mặt khác theo giả thiết ta có \(CD \bot AB.\)

Do đó \(AB//CE.\)

Mặt khác các dây \(CE,AB\) là hai dây song song của \(\left( O \right)\) chắn hai cung \(AC\) và \(BE\) nên

cung  \(AC\)  bằng cung \(BE\)  hay cùng \(AE\)  bằng cung \(BC\)  suy ra $EA = BC.$

Mặt khác \(\widehat {DAE} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).

Do đó \(M{A^2} + M{B^2} + M{C^2} + M{D^2} = \left( {M{A^2} + M{D^2}} \right) + \left( {M{B^2} + M{C^2}} \right) = A{D^2} + B{C^2} = D{E^2} = 4{R^2} = 4.\)

Áp dụng bất đẳng thức Cô-si cho \(M{A^2},M{B^2}\) ta có

\(M{A^2} + M{B^2} \ge 2MA.MB \Rightarrow 2\left( {M{A^2} + M{B^2}} \right) \ge 2M{A^2} + 2M{B^2} \ge M{A^2} + M{B^2} + 2MA.MB = {\left( {MA + MB} \right)^2}.\)

Tương tự

\(2\left( {M{C^2} + M{D^2}} \right) \ge {\left( {MC + MD} \right)^2}.\)

Bằng cách tương tự trên ta chứng minh được

\(2\left[ {{{\left( {MA + MB} \right)}^2} + {{\left( {MC + MD} \right)}^2}} \right] \ge {\left( {MA + MB + MC + MD} \right)^2}.\)

Từ đó ta suy ra \(4\left( {M{A^2} + M{B^2} + M{C^2} + M{D^2}} \right) \ge {\left( {MA + MB + MC + MD} \right)^2}.\) Vì vậy

\({\left( {MA + MB + MC + MD} \right)^2} \le 4.4 = {4^2} \Rightarrow MA + MB + MC + MD \le 4.\)

Dấu bằng xảy ra khi và chỉ khi \(MA = MB = MC = MD.\) Khi đó \(M \equiv O.\)