Câu hỏi:
2 năm trước
Cho đường tròn \(\left( {O;R} \right),\) đường kính \(AB\) cố định, đường kính \(CD\) thay đổi\(\left( {CD \ne AB} \right).\) Các tia \(BC,\,BD\) cắt tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) lần lượt tại \(E,\,F.\) Khi \(CD\) thay đổi. Giá trị nhỏ nhất của \(EF\) theo \(R\) là:
Trả lời bởi giáo viên
Đáp án đúng: a
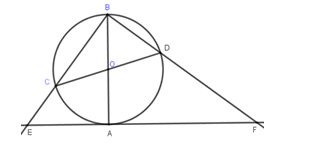
B\) thuộc đường tròn đường kính \(CD.\) Suy ra \(\widehat {DBC} = {90^0}.\)
Xét \(\Delta EBF\) có \(\widehat {EBF} = {90^0},\,BA \bot EF \Rightarrow AE.AF = A{B^2}\).
Theo bất đẳng thức Cô-si cho \(\left( {AE,AF} \right)\) ta có
\(EF = AE + AF \ge 2\sqrt {AE.AF} = 2\sqrt {A{B^2}} = 2AB = 4R.\)
Vậy giá trị nhỏ nhất của \(EF\) là \(4R.\) đạt được khi \(CD \bot AB.\)
Hướng dẫn giải:
Sử dụng hệ thức giữa đường cao và cạnh trong tam giác vuông để tính \(AE.AF = A{B^2}\).
Sử dụng bất đẳng thức Cô-si để tìm GTNN của $EF$.
