Cho hình vẽ ở bên. Biết rằng sđ\(BmC = {80^0},\) \(M\) là điểm chính giữa \(N\) và \(B,\)sđ$AqN = \dfrac{1}{2}$ sđ$NrC$

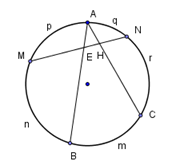
Khi đó ta có

Do tổng số đo tất cả các cung của đường tròn là \({360^0},\) hơn nữa ta có \(sd\,BmC = {80^0}\) nên ta có

\(sd\,BnM + sd\,MpA + sd\,AqN + sd\,NrC = {360^0} - {80^0} = {280^0}\,\,\left( 1 \right).\)

Mặt khác theo giả thiết ta cũng có

$\left\{ \begin{array}{l}sd\,MpA + sd\,AqN = sd\,BnM\,\left( 2 \right)\\sd\,AqN = \dfrac{1}{2}sd\,NrC\,\left( 3 \right)\end{array} \right..$

Thay \(\left( 3 \right)\) và \(\left( 2 \right)\) vào \(\left( 1 \right)\) ta nhận được

\({280^0} = sd\,BnM + \left( {sd\,MpA + sd\,AqN} \right) + 2sd\,AqN = 2\left( {sd\,BnM + sd\,AqN} \right).\) Từ đây ta có

\(sd\,BnM + sd\,AqN = {140^0}.\) Suy ra \(\widehat {HEA} = \dfrac{1}{2}\left( {sd\,BnM + sd\,AqN} \right) = {70^0}\,\,\left( 4 \right).\)

Hơn nữa ta suy ra từ \(\left( 1 \right)\) rằng

$\begin{array}{l}sd\,MpA + sd\,NrC = {280^0} - \left( {sd\,BnM + sd\,AqN} \right) = {280^0} - {140^0} = {140^0}\\ \Rightarrow \widehat {AHE} = \dfrac{1}{2}\left( {sd\,MpA + sd\,NrC} \right) = {70^0}\,\left( 5 \right).\end{array}$

Từ \(\left( 4 \right)\) và \(\left( 5 \right)\) suy ra \(\Delta AEH\) cân tại \(A\)